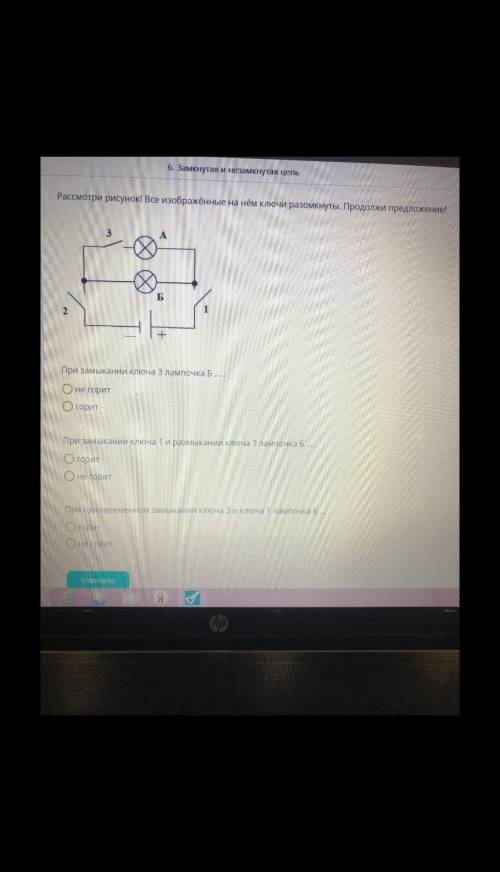
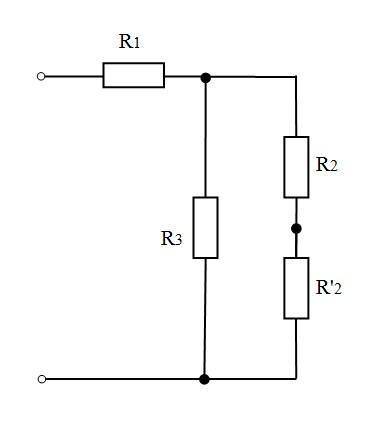
Схема состоит из:
группы сопротивлений R₂ и R₂', соединенных последовательно,
сопротивления R₃, соединенного параллельно с первой группой,
сопротивления R₁, соединенного последовательно с первыми двумя группами.
Преобразовать схему можно так: (см. рис.1)
Тогда общее сопротивление R₂ и R₂':
R₂₂ = R₂ + R₂' = 20 + 20 = 40 (Ом)
То есть сопротивления R₂ и R₂' можно заменить одним сопротивлением R₂₂ = 40 (Ом) (см. рис.2)
Общее сопротивление R₂₂ и R₃:
R₂₂₃ = R₂₂•R₃ : (R₂₂+R₃) = 40•60 : 100 = 24 (Ом)
Общее сопротивление цепи с учетом R₁:
R = R₁ + R₂₂₃ = 6 + 24 = 30 (Ом)
Общий ток в цепи:
I = I₁ = U/R = 240 : 30 = 8 (A)
Напряжение на первом сопротивлении:
U₁ = I · R₁ = 8 · 6 = 48 (B)
Напряжение на группе сопротивлений R₂₂₃:
U₂₂₃ = U - U₁ = 240 - 48 = 192 (B)
Ток, протекающий через R₃:
I₃ = U₂₂₃ : R₃ = 192 : 60 = 3,2 (A)
Ток, протекающий через R₂₂:
I₂₂ = U₂₂₃ : R₂₂ = 192 : 40 = 4,8 (A)
Напряжение на R₂ и R₂':
U₂ = U₂' = R₂I₂₂ = R₂'I₂₂ = 20 · 4,8 = 96 (B)
Это полезная задачка для освоения простых формул движения.
Пройденный путь равен скорость умножить на время: S = V * t.
Скорость стала в 2 раза меньше, т. е. V/2. Пройденный путь в 2 раза больше, т. е. 2S . И наша формула теперь выглядит так:
2S = V/2 * t.
Выразим отсюда t = 4S /V
А в первом случае t было равно t = S /V
Мы видим, что время движения стало в 4 раза больше, т. е. 40 минут.
Но это формальный решения. Задача сия проста, поэтому можно решить ее без формул (что и сделали авторы ответов) . Примерно так:
При увеличении расстояния вдвое время движения увеличится в 2 раза. Но за счет уменьшения скорости время движения тоже увеличивается в 2 раза. Значит, в итоге время увеличится в 2 * 2 = 4 раза.
Объяснение: