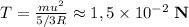
1) Водяной пар имеет большую температуру и большую внутреннюю энергию.
2) Вольфрам - самый тугоплавкий металл . Температура плавления больше трёх тысяч градусов Он останется твердым.
3) Температура замерзания спирта гораздо ниже чем у ртути.
4) Не будет. Тающий лёд имеет температуру 0 градусов. Эта температура будет поддерживаться пока весь снег не растает. Процесс теплопередачи пропорционален разности температур, поэтому лёд в пробирке не растает.
5) Аналогично предыдущему пункту вода не замёрзнет. Температура замерзания молоко на полградуса ниже нуля.
6) Растворение соли энергоёмкий процесс, поэтому температура при растворении понижается.
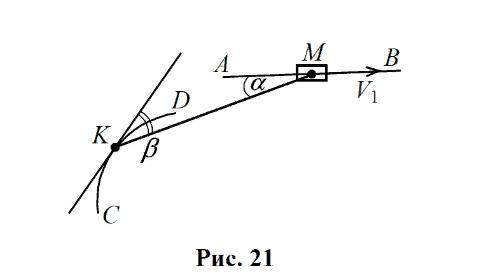
а) Примем, что нить нерастяжима в продольном направлении. Рассмотрим движение нити. Она двигается сложным образом: одновременно вращательно и поступательно. Выделим составляющие каждой скорости: проекции на нить и на направление, перпендикулярное нити. Равенство проекций скоростей на направление, перпендикулярное нити, необязательно: нить может "изгибаться", то есть компоненты скоростей, которые вращают нить, не влияют на длину нити, однако составляющие, спроецированные на нить, влияют — они стремятся растянуть эту нить в продольном направлении. Нужно потребовать их равенство: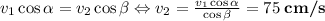
б) Прибавим к кольцу и муфте вектор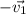 . Получим, что M неподвижна, а К движется по окружности с центром в точке M, поскольку расстояние между кольцом и муфтой постоянно. Поэтому вектор
. Получим, что M неподвижна, а К движется по окружности с центром в точке M, поскольку расстояние между кольцом и муфтой постоянно. Поэтому вектор 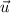 перпендикулярен прямой, содержащей нить (вектор мгновенной скорости всегда направлен по касательной к окружности). После нехитрой геометрии приходим к углу между вектором
перпендикулярен прямой, содержащей нить (вектор мгновенной скорости всегда направлен по касательной к окружности). После нехитрой геометрии приходим к углу между вектором 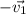 и вектором
и вектором 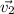 . Он равен
. Он равен 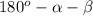 . Итак,
. Итак, 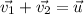 . Возводя в квадрат, получаем:
. Возводя в квадрат, получаем: 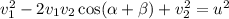 . После подстановки ранее найденных значений получаем
. После подстановки ранее найденных значений получаем 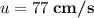 .
.
Впрочем, можно было и проще: заметим, что сумма проекции векторов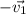 и
и 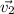 на прямую, содержащую нить, равна нулю. Поэтому, зная, что искомый вектор перпендикулярен этой прямой, можно сразу получить ответ:
на прямую, содержащую нить, равна нулю. Поэтому, зная, что искомый вектор перпендикулярен этой прямой, можно сразу получить ответ: 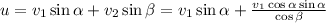
в) Перейдем в систему отсчета, связанную с муфтой. Центростремительное ускорение кольца равно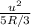 . Тогда искомая сила равна
. Тогда искомая сила равна