Формула бинома Ньютона является частным случаем разложения функции {\displaystyle (1+x)^{r}} (1+x)^r в ряд Тейлора:
{\displaystyle (1+x)^{r}=\sum _{k=0}^{\infty }{r \choose k}x^{k}} (1+x)^r=\sum_{k=0}^{\infty} {r \choose k} x^k,
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты этого разложения находятся по формуле:
{\displaystyle {r \choose k}={1 \over k!}\prod _{n=0}^{k-1}(r-n)={\frac {r(r-1)(r-2)\cdots (r-(k-1))}{k!}}} {\displaystyle {r \choose k}={1 \over k!}\prod _{n=0}^{k-1}(r-n)={\frac {r(r-1)(r-2)\cdots (r-(k-1))}{k!}}}
При этом ряд
{\displaystyle (1+z)^{\alpha }=1+\alpha {}z+{\frac {\alpha (\alpha -1)}{2}}z^{2}+...+{\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}z^{n}+...} (1+z)^\alpha=1+\alpha{}z+\frac{\alpha(\alpha-1)}{2}z^2+...+\frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}z^n+
сходится при {\displaystyle |z|\leq 1} |z|\le 1.
В частности, при {\displaystyle z={\frac {1}{m}}} z=\frac{1}{m} и {\displaystyle \alpha =x\cdot m} \alpha=x\cdot m получается тождество
{\displaystyle \left(1+{\frac {1}{m}}\right)^{xm}=1+x+{\frac {xm(xm-1)}{2\;m^{2}}}+...+{\frac {xm(xm-1)\cdots (xm-n+1)}{n!\;m^{n}}}+\dots .} \left(1+\frac{1}{m}\right)^{xm}=1+x+\frac{xm(xm-1)}{2\; m^2}+...+\frac{xm(xm-1)\cdots(xm-n+1)}{n!\; m^n}+\dots.
Переходя к пределу при {\displaystyle m\to \infty } m\to\infty и используя второй замечательный предел {\displaystyle \lim _{m\to \infty }{\left(1+{\frac {1}{m}}\right)^{m}}=e} \lim_{m\to\infty}{\left(1+\frac{1}{m}\right)^{m}}=e, выводим тождество
{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2}}+\dots +{\frac {x^{n}}{n!}}+\dots ,} e^x=1+x+\frac{x^2}{2}+\dots+\frac{x^n}{n!}+\dots,
которое именно таким образом было впервые получено Эйлером.
Ну, для начала, если вытянуть руку, держа при этом попрыгунчик, то потенциальная энергия порыгунчика будет на максимуме. При падении потенциальная энергия будет уменьшаться, а кинетическия увеличиваться(пропорцианально друг другу).
При столкновении с плоской поверхностью попрыгунчик отскочит благодоря набранной при полете силы ускорения(g= 9.8 м\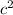 ) и силе упругости каучука(резина). Так же, если кинуть мячик под углом, то он отскочит прямо пропорционально этому углу(угол падения = углу отражения).
) и силе упругости каучука(резина). Так же, если кинуть мячик под углом, то он отскочит прямо пропорционально этому углу(угол падения = углу отражения).
Ну вот, "пища" для размышления есть, как бы образец :)
Удачи.