Объяснение:
Дано:
λ = 450 нм = 450·10⁻⁹ м
λкр = 600 нм = 600·10⁻⁹ м
V - ?
1)
Находим энергию:
ε = h·c / λ
2)
Находим работу выхода:
A вых = h·c / λкр
3) Находим кинетическую энергию фотоэлектрона:
W = m·V² / 2
4)
Записываем формулу Эйнштейна для фотоэффекта:
ε = Авых + W
h·c / λ = h·c / λкр + m·V² / 2
m·V² / 2 = h·c / λ - h·c / λкр
m·V² / 2 = h·c ( 1/ λ - 1 / λкр)
V² = 2·h·c ( 1/ λ - 1 / λкр)/m
V² = 2·6,63·10⁻³⁴·3·10⁸· (1/(450·10⁻⁹) - 1/(600·10⁻⁹)) / (9,1·10⁻³¹) ≈
≈ 2,43·10¹¹ (м/с)²
V = √ (2,43·10¹¹) ≈ 4,9·10⁵ м/с
№1.
По уравнению Эйнштейна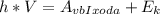
, где V - частота излучения (Гц), h - постоянная планка (h = 6,62*10⁻³⁴ Дж*с), 
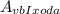- работа выхода (Дж), 
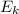- максимальная энергия излучения (Дж). Из данной формулы выражаем находимую кинетическую энергию: 
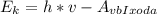. В системе СИ: 4,4 эВ = 4,4*1,1*10⁻¹⁹ Дж = 7,04*10⁻¹⁹ Дж. Подставляем численные данные и вычисляем:
ответ: Кинетическая энергия равна 390,16*10⁻¹⁹ Джоуль.
№2.
По формуле фотоэффекта (из закона сохранения энергии)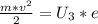
, где m - масса частицы (кг), 
- скорость частицы (м/с), e - заряж электрона (e = 1,6*10⁻¹⁹ Кл), U₃ - запирающие напряжение т.е. напряжение при котором ток полностью прекращается (В). Выражение: ![\frac{m*v^2}{2}[tex] есть кинетическая энергия т.е. [tex]E_k=\frac{m*v^2}{2}[tex]. В задаче №1 если взглянуть есть формула полученая в ходе преобразования (кинетической энергии) ⇒ [tex]E_k=h*v-A_{vbIxoda}](/tpl/images/0148/7389/40de7.png)
. Тогда кинетическую энергию расписываем как: