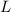Два тела движутся в разные стороны. Начертите ось справа налево. За единичный отрезок примите одну клетку. Начальная координата первого тела минус 2 метра, координата второго 6 метров. Скорость первого
направлена слева направо и равна 5 метров в секунду, скорость второго – 3 метра в секунду. Запишите
уравнения движения для обоих тел. Определите момент и место встречи этих тел. Определите на каком
расстоянии они будут друг от друга через 8 секунд после начала движения.

👇

Открыть все ответы

Ответ:

Гуманитарийлох

17.03.2021

В однородном гравитационном поле все тела, двигающиеся под действием силы тяжести, испытывают одно и то же ускорение, определяемое исключительно параметром поля (если, конечно, пренебречь сопротивлением среды и взаимным притяжением тел). Это означает, что в неинерциальной системе отсчёта, связанной с ЛЮБЫМ таким телом, все подобные тела двигаются прямолинейно и равномерно.
Данную задачу удобно решать в неинерциальной системе, связанной с телом Б и вести отсчёт с момента начала свободного падения с высоты Н.
Скорость тела А в момент броска в системе Б есть константа и равна
v = Δx/t = (H - h)/t = (10 - 6)/0.16 = 25 м в сек
Время встречи
t₀ = H/v = 10/25 = 0.4 c
PS
Проверим справедливость наших расчётов в более привычной системе, связанной с Землёй.
Для тела А
x1 = vt₀ - gt₀²/2 = 25*0.4 - 10*0.4²/2 = 10 - 0.8 = 9.2 м
Для тела Б
x2 = H - gt₀²/2 = 10 - 10*0.4²/2 = 10 - 0.8 = 9.2 м
x1 = x2 тела встретились, значит наши рассуждения правильны.

4,8(79 оценок)

Ответ:

matievskaya79

17.03.2021

Если есть проблемы с отображением, смотрите снимок ответа, приложенный к нему.
===
Смотрите рисунок к задаче, который прикрелпен к ответу. В задаче нас просят найти

— расстояние от места пуска ядра до места его падения, причем пуск ядра производился с холма, на высоте 20 m

.
Движение происходит на плоскости с координатными осями x, y

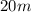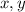, соответственно все характеристики движения будем производить, опираясь на эти оси. Переведем все характеристики в вид проекций на эти оси: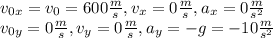
$v_{0x} = v_0 = 600 \frac{m}{s}, v_x = 0 \frac{m}{s}, a_x = 0 \frac{m}{s^2} \\ 
v_{0y} = 0 \frac{m}{s}, v_y = 0 \frac{m}{s}, a_y = -g = -10 \frac{m}{s^2}$
Условимся, что снаряд в конце своего движения оказывается на земле, то есть на высоте, равной нулю. Значит перемещение вдоль оси

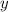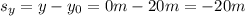будет равно s_y = y - y_0 = 0 m - 20 m = -20 m

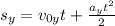. Это перемещение можно описать по формуле $s_y = v_{0y}t + \frac{a_yt^2}{2}$ , подставим все известные значения:
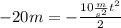
$-20 m = -\frac{10\frac{m}{s^2}t^2}{2} \\ 
$
Отсюда выразим время движения снаряда:
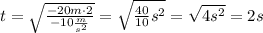
$t = \sqrt{\frac{-20 m \cdot 2}{-10 \frac{m}{s^2}}} = \sqrt{\frac{40}{10} s^2} = \sqrt{4 s^2} = 2 s$
Итак, имеем, что движение снаряда происходило в течение двух секунд.
Дальность снаряда — это перемещение вдоль оси

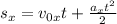. Его можно описать по формуле $s_x = v_{0x}t + \frac{a_xt^2}{2}$ . Подставим все известные значения:
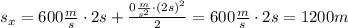
$s_x = 600 \frac{m}{s} \cdot 2 s + \frac{0 \frac{m}{s^2} \cdot (2s)^2}{2} = 600 \frac{m}{s} \cdot 2 s = 1200 m$
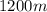Имеем, что дальность полета составляет 1200 m

. Отмечу, что это дальность полета в вакууме, поскольку при расчетах мы не учли сопротивление воздуха (а оно при таких скоростях очень велико), но в условии задачи дано, сколько процентов от дальности полета в вакууме составляет дальность полета в воздушной среде. Найдем теперь дальность полета в воздушной среде: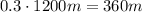
$0.3 \cdot 1200 m = 360 m$
Перемещение вдоль оси

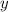не изменилось (так как снаряд «упал» с высоты 20 метров до нуля). Из рисунка видно, что искомая удаленность пушки от места приземления снаряда —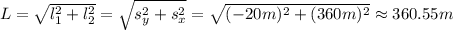 $L = \sqrt{l_1^2 + l_2^2} = \sqrt{s_y^2 + s_x^2} = \sqrt{(-20m)^2 + (360m)^2} \approx 360.55 m$
Это ответ.

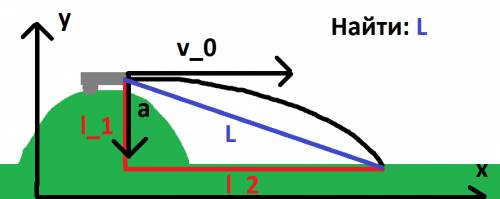
На холме высотой 20 м установлено орудие и произведен выстрел в горизонтальном направлении. на каком