1)Для того чтобы вычислить начальную скорость первого тела нужно знать время падения этого тела.а время падения можно вычислить для второго тела они будут одинаковы т.к. одновременно начали движение и одновременно приземлились. Для второго тела время будет вычисляться по формуле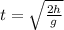 
. получим время падения первого и второго тела равно t=3.2 c. Используя формулу пройденного пути при свободном падении 
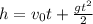, выразим v0. Получим 
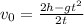. Подставив все числа получим v0=9.75 м/с
2) Сначала вычислим высоту на которую поднимется камень после броска h=v0t-gt^2/2. тут нам неизвестно время.его мы модем найти из формулы скорости. конечная скорость будет равна нулю,т.к. тело поднимется-остановится и потом начнет падать вниз.V0=gt отсюда t=v0/g, t=8/10=0.8 c. Подставляем в формулу для высоты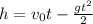 
получим h2=8*0,8-(10*0,64)/2=3,2 м. Теперь плюсуем эту высоту с той,которая нам дана и получаем общую высоту с которой падает тело на землю. h=h1+h2 h=28+3.2=31.2м. Для того чтобы вычислить скорость падения воспользуемся уже знакомой на формулой v=v0+gt, в данном случае v0=0, т.к. тело перед тем как начать падать-остановилось. получаем v=gt. вычислить время падения с высоты 31,2 м можно из формулы 
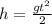. Тогда 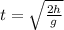, Подставив числа получим время всего падения равно t=5,6 с. Подставив это время в формулу скорости получим v=10*5,6=56 м/с
Масса инерционная и масса гравитационная - это две разные характеристики тела. И гравитационная постоянная точно учитывается при расчёте гравитационной массы. Учитывается ли она при расчёте инерционной массы?
Когда Ньютон сформулировал свой закон всемирного тяготения, он обнаружил, что тот вполне себе соответствует другому главному закону, который мы сегодня знаем как Второй закон Ньютона:
F = m*a.
То есть, если приравнять два закона, то получится:
F = GMm / R²
F = m_i*a
F = F => G*M*m_g / R² = m_i*a => m_g*(G*M / R²) = m_i*a.
Ньютон получил две массы: гравитационную - слева, и инертную (инерционную) - справа. Но в то время никто не мог сказать, что эти массы можно считать одним и тем же. Это сегодня мы запросто сокращаем массы слева и справа, когда получаем такое уравнение.
Однако было проведено множество опытов, доказывающих, что ускорение "а" во Втором законе Ньютона, если сопоставлять этот закон с законом всемирного тяготения, абсолютно идентично ускорению свободного падения, которым является выражение "G*M / R²". Абсолютно идентично ДЛЯ ВСЕХ ТЕЛ. То есть:
m_i*a = m_g*(G*M / R²) = m_g*g.
А раз ускорения одинаковые, то и массы одинаковые. А раз это так, то их можно не разделять на гравитационную и инертную.
Получается, что массы стали считать одним и тем же только после того, как доказали равенство ускорений. А если ускорение "g" - это то же самое, что "G*M / R²", куда входит гравитационная постоянная, и то же самое, что "а", то ответ на вопрос - да, учитывается.