Дано:
U = 4 кВ = 4000 В
d = 20 см = 0,2 м
E - ?
E = U / d
E = 4000 В / 0,2 м = 20000 В/м = 20 кВ/м
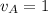 м/с
м/с
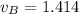 м/с
м/с
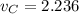 м/с
м/с
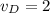 м/с
м/с
Объяснение:
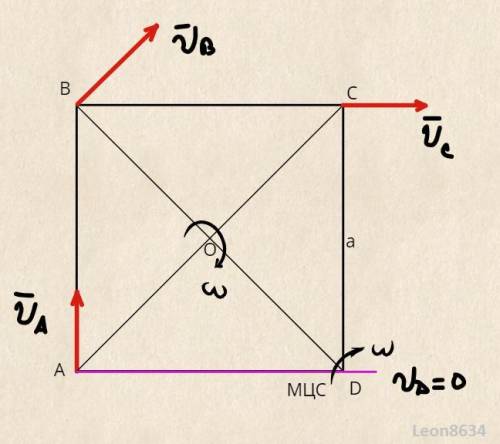
Точка Е на рисунке - мгновенный центр скоростей. Рассчитаем радиальную скорость точки А
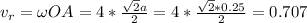 м/с
м/с
Рассчитаем скорость поступательного движения точке пластины по теореме косинусов (учтем что угол между красным и синим вектором 45°)
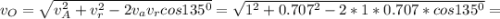
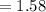 м/с
м/с
Угол ОЕА совпадает с углом между зеленым и красным векторами (все рассуждения сейчас относятся к точке А), найдем его по теореме синусов
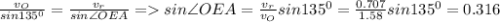
Опустим перпендикуляр с точки О на сторону AD его длина равна a/2=12.5 см, он же катет в прямоугольном треугольнике. Тогда легко найти отрезок ЕО (по совместительству радиус вектор точки О)
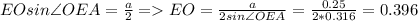 м
м
Угловая скорость относительно точки Е
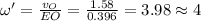 рад/с (все эти выкладки были для доказательства равенства угловых скоростей относительно точек E и O, их можно опустить). Теперь все совсем просто
рад/с (все эти выкладки были для доказательства равенства угловых скоростей относительно точек E и O, их можно опустить). Теперь все совсем просто
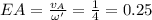 м
м
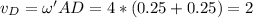 м/с
м/с
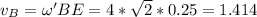 м/с
м/с
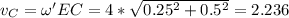 м/с.
м/с.
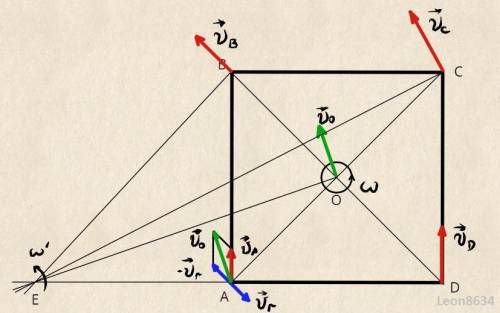
Для случая, когда направление вращения совпадает с направлением обхода:
0; 1; 1,41
Для случая, когда направление вращения противоположно направлению обхода:
1,41; 2; 2,24
Объяснение:
Определим положение мгновенного центра скоростей. Очевидно, он лежит на перпендикуляре к скорости 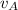 . Расстояние до него:
. Расстояние до него:
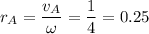 м
м
Значит, мгновенный центр скоростей совпадает с вершиной D квадрата.
Скорости остальных вершин:
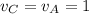 м/с
м/с
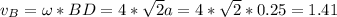 м/с
м/с
Для случая вращения против направления обхода вершин задача была решена мной 26.07.2020, значения скоростей прикрепляю в шапку.
Запишем формулу напряжённости электрического поля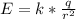 и формулу потенциала электрического поля
и формулу потенциала электрического поля 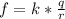 . Данные формулы почти индентичны, нехватает только в формуле потенциала электрического поля квадрата растояния. Выражаем напряжённость электрического поля через потенциал электрического поля т.е. формулу напряженности представляем как
. Данные формулы почти индентичны, нехватает только в формуле потенциала электрического поля квадрата растояния. Выражаем напряжённость электрического поля через потенциал электрического поля т.е. формулу напряженности представляем как 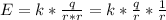 где выражение
где выражение  есть потенциал электрического поля. Заменив получим
есть потенциал электрического поля. Заменив получим 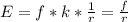 . Напряжение - это и есть разность потециалов т.е.
. Напряжение - это и есть разность потециалов т.е. 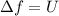 , то
, то 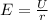 . В системе СИ:
. В системе СИ:
20 см = 0,2 м; 4 кВ = 4000 В. Подставляем численные данные и вычисляем: