Объяснение:
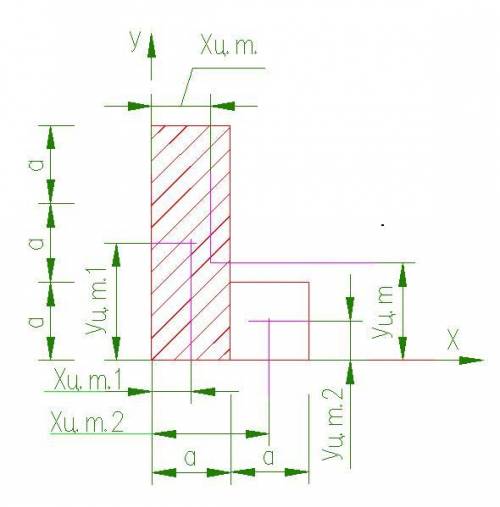
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
главное-нарисовать. как то так:
__A
|\
B1| \
B | / С
| /
|/
|
D
нарисовать конечно лучше надо, особенно угол DAC чтобы равен 60 градусам был.
А теперь смотрим: между двумя нарисоваными горизонтальными прямыми и есть однородное электрическое поле с напряженностью E=600В/м.
Точка, про которую говорится в задаче- это точка В, и она лежит на векторе AD, который перепендикулярен нарисованым вначале прямым.
Смотрим на условие, где говорится, что угол между AD и AC равен 60 градусам ( то есть DAC=BAC=60градусов).
Расстояние 2 мм (BC)- это кратчайшее растояние между точками на обозначеных прямых, а значит AB=AC, и треугольник ABC оказывается равносторонним, все стороны у него по 2мм а углы по 60 градусов.
И в нем что хорда, что биссектриса, что меридиана все одно и тоже. Ну и опустим ( нарисуем) их из вершины C треугольника ABC, получатся отрезки AB1= B1B= 2мм/2=1мм. И расстояние проекции искомых точек на вектор напряженности=1мм.
А значит напряжение между этими точками равно
U= 600В/м*1мм=(600В/1м)*(1/1000м)=0,6В.
Дано: m=3кг; L=2,3*10^6Дж/кг; Q - ?
Q=Lm=3*2,3*10^6=6,9*10^6Дж=6,9 МДж - это ответ.
Объяснение: