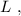 и жёсткостью
и жёсткостью 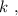 деформацию которой обозначим, как
деформацию которой обозначим, как 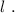 Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука:
Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука: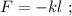
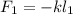
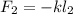

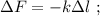
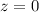 – все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на
– все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на 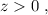 (т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как:
(т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как: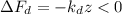 – это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.
– это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.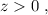 (вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как:
(вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как: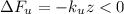 – это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.
– это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.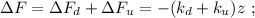
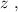 общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил:
общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил: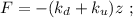
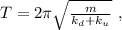 где
где 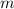 – масса шарика.
– масса шарика.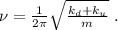
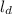 (нижней), и
(нижней), и 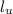 (верхней). При этом положим вертикальное положение груза
(верхней). При этом положим вертикальное положение груза  Ось
Ось 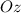 направлена вверх.
направлена вверх.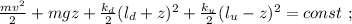
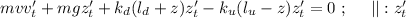
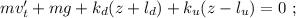
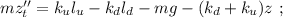
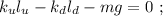
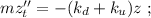
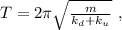 где
где 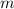 – масса шарика.
– масса шарика.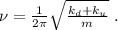
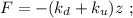
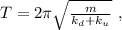 где
где 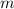 – масса шарика.
– масса шарика.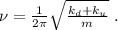
 Н/см
Н/см 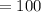 Н
Н 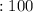 см
см 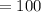 Н
Н 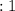 м
м 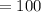 Н/м ;
Н/м ;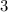 Н/см
Н/см 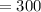 Н
Н 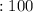 см
см 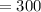 Н
Н 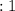 м
м 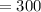 Н/м ;
Н/м ;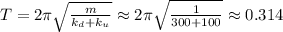 сек ;
сек ;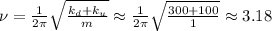 Гц .
Гц .
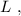 и жёсткостью
и жёсткостью 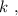 деформацию которой обозначим, как
деформацию которой обозначим, как 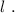 Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука:
Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука: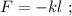
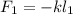
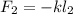

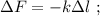
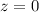 – все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на
– все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на 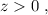 (т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как:
(т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как: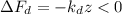 – это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.
– это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.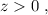 (вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как:
(вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как: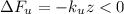 – это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.
– это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.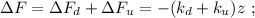
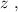 общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил:
общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил: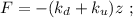
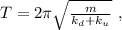 где
где 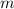 – масса шарика.
– масса шарика.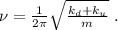
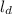 (нижней), и
(нижней), и 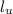 (верхней). При этом положим вертикальное положение груза
(верхней). При этом положим вертикальное положение груза  Ось
Ось 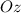 направлена вверх.
направлена вверх.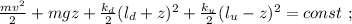
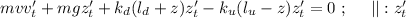
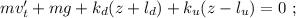
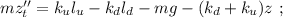
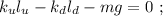
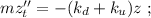
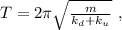 где
где 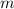 – масса шарика.
– масса шарика.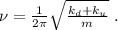
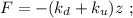
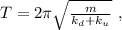 где
где 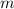 – масса шарика.
– масса шарика.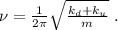
 Н/см
Н/см 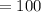 Н
Н 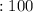 см
см 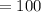 Н
Н 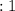 м
м 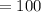 Н/м ;
Н/м ;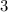 Н/см
Н/см 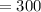 Н
Н 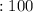 см
см 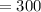 Н
Н 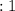 м
м 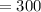 Н/м ;
Н/м ;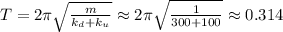 сек ;
сек ;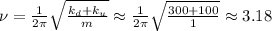 Гц .
Гц .
ействие одного тела на другое не может быть односторонним.
Если первое тело действует на второе, то и второе действует на первое.
В результате взаимодействия оба тела могут изменить форму или скорость.
Мерой воздействия оба тела могут изменить свою форму или скорость.
Мерой воздействия одного тела на другое является силой. Сила векторная величина.
На чертеже силу изображают в виде отрезка прямой со стрелкой на конце, при этом:начало отрезка есть точка приложения силы.
направление стрелки указывает направление силы.
длина отрезка условно обозначает в некотором масштабе модуль силы
рядом со стрелкой пишется обозначает вектор F
Объяснение: