При уменьшении длины пружины её жёсткость увеличивается.
Объяснение:
Конструкторская формула для расчёта жесткости цилиндрической пружины, изготовленной из круглого прутка пружинной стали
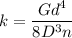
здесь k - жесткость пружины (Н/мм), G - модуль сдвига (МПа), d - диаметр проволоки (прута, мм), D - средний диаметр (разность внешнего диаметра пружины и диаметра проволоки, мм), n - количество рабочих витков.
Какова же связь с длиной пружины?
Чем больше длина пружины L, тем больше витков n содержит она.
Чем больше витков n при прочих одинаковых характеристиках, тем жесткость k пружины меньше.
Следовательно, при уменьшении длины пружины её жёсткость увеличивается.
a ≈ 66.058 м/с²
α ≈ 0,243°
Объяснение:
φ(t) = 7t + 0.8t² - угол поворота маховика
D = 0.35 м - диаметр маховика
v₁ = 3 м/с - скорость точки обода маховика в момент t₁
a - ? - ускорение точки обода в момент t₁
α₁ - ? - угол между вектором ускорения точки и радиусом
------------------------------------------------------------------
Закон изменения угловой скорости маховика
ω(t) = φ'(t) = 7 + 1.6t
Закон изменения углового ускорения маховика
ε(t) = ω'(t) = 1.6 (рад/с²)
Угловое ускорение постоянно, следовательно вращение равноускоренное
Радиус маховика
R = 0.5 D = 0.5 · 0.35 = 0.175 (м)
Cкорость точки маховика
v(t) = ω(t) · R = 0.175 ω(t)
По условию в момент времени t₁
0.175 · ω(t₁) = 3.4
Угловая скорость в момент времени t₁
ω(t₁) = 3.4 : 0.175 ≈ 19.43 (рад/с)
Центростремительное ускорение точки в момент времени t₁
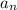 = ω²(t₁) · R = 19.43² · 0.175 ≈ 66.057 (м/с²)
= ω²(t₁) · R = 19.43² · 0.175 ≈ 66.057 (м/с²)
Касательное ускорение точки \
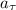 = ε · R = 1.6 · 0.175 = 0.28 (м/с²)
= ε · R = 1.6 · 0.175 = 0.28 (м/с²)
Модуль полного ускорения точки
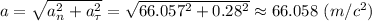
Угол α между вектором полного ускорения точки и радиусом
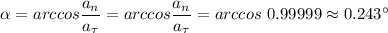
РЕШЕНИЕ
mv=Ft
v=Ft/m=0.1H*5c/0.2кг=2.5м/с
Объяснение: УЧИ уроки