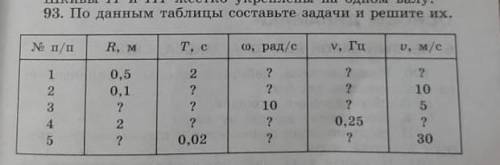
Пусть S - длина одного вагона, t - время, за которое второй вагон проехал мимо пешехода, а tₓ - искомое время.
Формулы для равноускоренного движения:
 (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)
(ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)
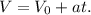 (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)
(ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)
Зная, что начальная скорость V₀ = 0, получаем:
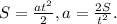
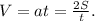
Когда пешеход будет стоять у начала десятого вагона (назовём это момент 1, скорость в этот момент соответственно V₁), то возле него проедет уже 8 вагонов (с 2-ого по 9-ый), длина 8 вагонов S₁ = 8S.
Вспомним формулу не требующую наличие времени:
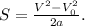 (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)
(ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)
Для нашей задачи, учитывая, что V₀ = 0, формула имеет вид:
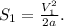
Тогда отсюда скорость V₁
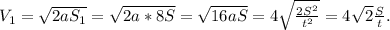
Рассмотрим момент, когда пешеход будет стоять уже у конца 10-ого вагона (назовём это момент 2, скорость в этот момент соответственно V₂), тогда возле него проедет уже 9 вагонов, длина 9 вагонов S₂ = 9S.
Выразим скорость V₂:
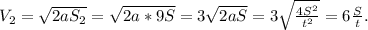
Используя формулу 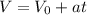 (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ) для скоростей V₁ и V₂ найдём нужное нам время tₓ.
(ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ) для скоростей V₁ и V₂ найдём нужное нам время tₓ.
Формула примет следующий вид:
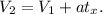
Отсюда искомое время tₓ:
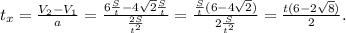
Найдём окончательный численный ответ, подставив t = 5 с:
 (c).
(c).
Таким образом мы получили tₓ = 0,9 с.
ответ: 0,9 секунд.
Формулы "общего вида" своей символикой не имеют отношения к задаче, они просто выписаны в качестве "опоры".
предположим, что высоту h = 20 м измерили относительно точки соударения тела с наклонной плоскостью. тогда из закона сохранения полной механической энергии скорость, с которой тело соударяется, равна v = √[2gh]
раз удар абсолютно упругий, то тело отразится под таким же углом, под каким падало
нужно провести перпендикуляр к точке соударения. угол между перпендикуляром и вертикалью равен α = 45°. такой же угол, отложенный от перпендикуляра, - есть направление, по которому направлен вектор скорости после соударения (его величина при этом не меняется, т.к. удар абсолютно упругий - время соударения мало и тепла не выделяется)
горизонтальная составляющая скорости тела в начальный момент времени после соударения равна v0(x) = v cos(90° - 2α) = v
в дальнейшем в силу отсутствия сил в проекции на горизонтальную ось v0(x) = const для любого момента времени
v(x) = √[2gh] = 20 м/c