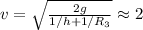 км/с .
км/с .
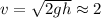 км/с ;
км/с ;
Объяснение:
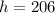 км
км 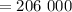 м – максимальная высота подъёма ;
м – максимальная высота подъёма ;
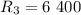 км
км 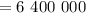 м – радиус Земли ;
м – радиус Земли ;
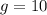 м/c² – ускорение свободного падения на поверхности ;
м/c² – ускорение свободного падения на поверхности ;
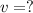 – найти начальную скорость.
– найти начальную скорость.
Далее в решении мы никак не будем учитывать вращение Земли, поскольку дело происходит на полюсе, где линейная скорость вращения поверхности земли относительно её центра пренебрежимо мала.
Потенциальная энергия гравитационного взаимодействия тел, когда её общее изменение необходимо учесть на расстояниях, отличающихся на величину, соизмеримую с радиусом Земли, описывается выражаением:
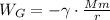 , где
, где 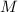 и
и 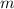 – большое и малое гравитирующие тела, а
– большое и малое гравитирующие тела, а  – расстояние между ними.
– расстояние между ними.
Правильность такого расчёта легко проверить следующим образом. Пусть тела находятся на расстоянии 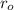 , а затем под действием гравитации приближаются на расстояние
, а затем под действием гравитации приближаются на расстояние 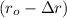 . Значит их потенциальная энергия уменьшится со значения
. Значит их потенциальная энергия уменьшится со значения 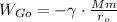 , до значения
, до значения 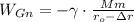 . Падение потенциальной энергии таким образом (равное росту кинетической):
. Падение потенциальной энергии таким образом (равное росту кинетической):
![\Delta W_{G} = W_{Go} - W_{Gn} = [ - \gamma \cdot \frac{Mm}{r_o} ] - [ - \gamma \cdot \frac{Mm}{ r_o - \Delta r } ] =](/tpl/images/1010/4229/1dea4.png)
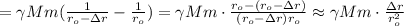 ;
;
(*) 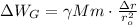 ;
;
Но с другой стороны, падение потенциальной энергии равно работе гравитационного поля:
(**) 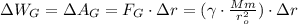 ;
;
Как легко видеть, выражения (*) и (**) – равны, что доказывает справедливость описания потенциальной энергии гравитационного взаимодействия выражением:
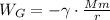 ;
;
Общая механическая энергия (вместе с кинетической 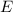 ) в верхней точке будет такой же, какой была в нижней, за вычетом
) в верхней точке будет такой же, какой была в нижней, за вычетом 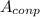 работы сил сопротивления среды (атмосферы):
работы сил сопротивления среды (атмосферы):
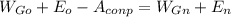 ;
;
Поскольку сопротивление мы не учитываем (пренебрегаем), то уравнение принимает вид:
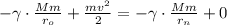 ;
;
Умножим на 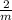 :
:
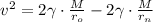 ;
;
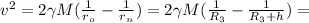
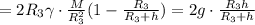 ;
;
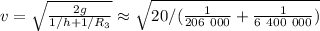 м/с
м/с 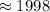 м/с
м/с 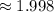 км/с
км/с 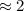 км/с .
км/с .
Мы пренебрегли сопротивлением воздуха, так что вычислять так точно падение потенциальной энергии с учётом меняющегося 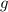 не имеет практического смысла. Можно посчитать то же самое и по более простому, приближённому алгоритму:
не имеет практического смысла. Можно посчитать то же самое и по более простому, приближённому алгоритму:
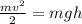 ;
;
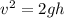 ;
;
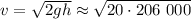 м/с
м/с 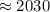 м/с
м/с 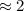 км/с ;
км/с ;
*** Вообще, всё выглядит немного странно, тут подозрительно странным числом указана высота. К чему это 206? Возможно в исходном условии было: 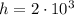 км
км 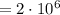 м.
м.
Тогда бы верное решение получалось только первым
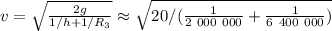 м/с
м/с 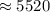 м/с
м/с 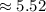 км/с
км/с 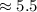 км/с .
км/с .
В упрощённом варианте подсчёта при этом была бы уже значительная ошибка:
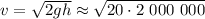 м/с
м/с 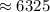 м/с
м/с 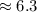 км/с .
км/с .
g = 9.81
1)Расстояние между мальчиком и стеной - перпендикуляр от мальчика к стенке ,т.е. пройденное путь по x. Проекция скорость на ось OX равна Vx = V * cos(a) (V - скорость мяча ,a - угол по которым кидают мяч) . Пройденный путь соответственно равен S = Vx * t = V*cos(a) * t = 8.7 м
2) Стоит рассмотреть случай ,если мяч ударяется о горизонтальную стенку . Тогда проекция скорости на ось OY , Vy = V * sin(a) ( (V - скорость мяча ,a - угол по которым кидают мяч ) .Пройденный путь соответственно равен S = Vy*t - gt^2/2 ( Уравнение ускоренного движения ) S = V*sin(a) * t - gt^2/2 = 8.8 м
ответ : 8.7 м ; 8.8 м