Объяснение:
1. по изображенным на рисунке 35 многоугольникам сил решите, сколько сил входит в каждую систему и какая из них уравновешена (обратите внимание на направление векторов)?
а) 4 силы, НЕ уравновешена
б) 5 сил, уравновешена
2. в каком случае задача на равновесие плоской системы сходящихся сил является статически определимой?
2) когда неизвестны величины (модули) двух сил;
два уравнения - две силы
3. какой вектор на рисунке 35,а является равнодействующей?
вектор OD
4. при каком значении угла a в соответствии с рисунком 36 (в пределах 00….1800) проекция силы F на указанную ось, будет равна:
1) нулю; <a = 90°
2) F; <a = 0°
3) – F. <a = 180°
д) в соответствии с рисунком 37 можно ли определить знак проекции силы F на показанную ось?
НАПРАВЛЕНИЕ ОСИ не задано, поэтому знак проекции силы F на показанную ось определить нельзя
5. укажите на рисунке 37 направление оси, при котором проекция силы F будет положительной?
направление оси НАЛЕВО от нас
6. на рисунке 38 определите проекцию равнодействующей системы на горизонтальную ось Х, если F1 = F2 = F3 = 10 Н.
Fpx = F1x +F2x +F3x = 0 + 10 + 10 *cos60 = 10 +10*1/2 =10 +5 =15
7. в каком случае плоская система сходящихся сил уравновешена?
3) Rх = 0, Rу = 0.
8. точка А, показанная на рисунке 39,а находится в равновесии под действием четырех сил, из которых силы R1 и R2 неизвестны. При каком расположении координатных осей (случай а или б ) полученные уравнения равновесия окажутся проще?
б) потому что ось Х сонаправлена с R1
9.определите модуль и направление равнодействующей силы системы сходящихся сил, если проекции слагаемых векторов равны:
Р1Х = 50 Н; Р2Х = - 30 Н; Р3Х = 60 Н; Р4Х = 70 Н;
Р1У = - 70 Н; Р2У = 40 Н; Р3У = 80 Н; Р4У = - 90 Н;
модуль равнодействующей силы определяем по формуле
|P| = √ [ Px² +Py²]
направление равнодействующей силы определяем по формуле
<a = arctg [Py/Px]
|P1| = 10√74 ; <a = -54,46°
|P2| = 50 ; <a = -53,13°
|P3| = 100 ; <a = 53,13°
|P4| = 10√130 ; <a = -52,13°
10. из представленных на рисунке 40 силовых треугольников, выберите треугольник, построенный для точки А. Шар подвешен на нити и находится в равновесии. Обратить внимание на направление реакции от гладкой опоры и условие равновесия шара.
НЕ представлен рисунок 40
Пройденный путь 8,5 м; модуль перемещения 2,5 м;
1-й этап движения
t₀ = 0; v₀ = 2 м/с;
t₁ = 1 с; v₁ = 3 м/с
Расчёт:
Δt₁ = t₁ - t₀ = 1 - 0 = 1 (c);
Δv₁ = v₁ - v₀ = 3 - 2 = 1 (м/c);
На 1-м этапе движение равноускоренное с ускорением
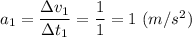
по закону
x₁(t) = 2t + 0.5t²
Считаем, что в начальный момент движения координата x₁(0) = 0
В момент времени t₁ = 1 c координата x₁(1) = 2·1 + 0.5·1² = 2.5 (м)
Движение происходит в сторону увеличения координаты.
Перемещение
r₁ = x₁(1) - x₁(0) = 2.5 - 0 = 2.5 (м)
Пройденный путь за этап
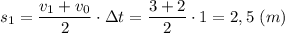
2-й этап движения
t₁ = 1 с; v₁ = 3 м/с
t₂ = 3 с; v₂ = 0;
Расчёт:
Δt₂ = t₂ - t₁ = 3 - 1 = 2 (с);
Δv₂ = v₂ - v₁ = 0 - 3 = -3 м/c;
На 2-м этапе движение равнозамедленное с ускорением
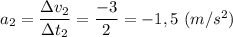
по закону
x₂(t) = 2.5 + 3 · (t - t₁) - 0.75 · (t - t₁)²
В момент времени t₂ = 3 c координата
x₂(3) = 2.5 + 3 · 2 - 0.75 · 2² = 5.5 (м)
Движение происходит в сторону увеличения координаты.
Перемещение к концу этапа
r₂ = x₂(3) - x₁(0) = 5.5 - 0 = 5.5 (м)
Пройденный путь за этап
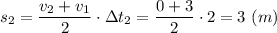
Пройденный путь за 2 этапа
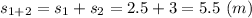
3-й этап движения
t₂ = 3 с; v₂ = 0;
t₃ = 6 с; v₃ = -1 м/с
Расчёт:
Δt₃ = t₃ - t₂ = 6 - 3 = 3 (с);
Δv₃ = v₃ - v₂ = -1 - 0 = -1 м/c;
На 3-м этапе движение равноускоренное с ускорением
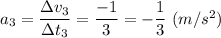
по закону
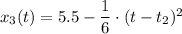
В момент времени t₃ = 6 c координата
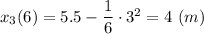
Движение происходит в сторону уменьшения координаты.
Перемещение к концу этапа
r₃ = x₃(6) - x₁(0) = 4 - 0 = 4 (м)
Пройденный путь за этап
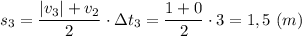
Пройденный путь за 3 этапа
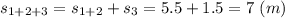
4-й этап движения
t₃ = 6 с; v₃ = -1 м/с
t₄ = 9 с; v₄ = 0;
Расчёт:
Δt₄ = t₄ - t₃ = 9 - 6 = 3 (с);
Δv₄ = v₄ - v₃ = 0 + 1 = 1 м/c;
На 3-м этапе движение равнозамедленное с ускорением
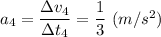
по закону
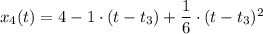
В момент времени t₄ = 9 c координата
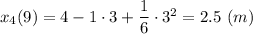
Движение происходит в сторону уменьшения координаты.
Перемещение к концу этапа
r₄ = x₄(9) - x₁(0) = 2.5 - 0 = 2.5 (м)
Пройденный путь за этап

Путь, пройденный за всё время движения
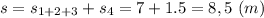
F=k*q1*q2 / r^2
r=√k*q1*q2 / F