3 закон Ньютона: Т - mxg = 0 (за ось взято направление вектора Т)
mx - масса свешивающегося "хвоста" (часть верёвки находящаяся ниже x и тянущая данную точку вниз с силой mxg) относительно данной точки. Т пропорциональна величине "хвоста" и как следствие максимальна у начала верёвки (х=0 м) и минимальна у её конца (Т=0 => х=2 м).
L = 2-0 = 2 м
3 закон Ньютона: Tмакс - mg = 0
m = Tмакс/g = 0.8/10 = 0.08 кг = 80 гр
Lв = 2 - 1.5 = 0.5 м - свешивающаяся часть верёвки относительно данной точки
Составим пропорцию, чтобы найти массу "хвоста" mx:
0.08/2 = mx/0.5
3 закон Ньютона: Tx - mxg = 0 => Tx = 0.2 Н
Дано:
F = 4 см
f = 12 см
Δs = 3 см
ΔS - ?
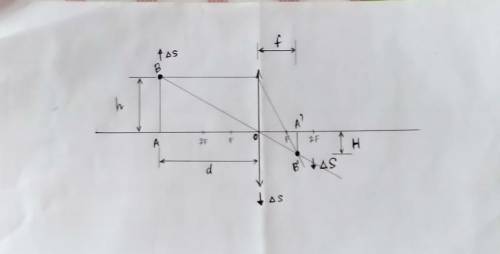
При данных условиях - точка на расстоянии 12 см, т.е. больше двойного фокусного расстояния (12 см > 2*4 см), и выше оптической оси - изображение точки находится на расстоянии гораздо меньшем от оси, причём располагается под осью, т.к. является перевёрнутым. Мы можем опустить перпендикуляры от точки до оси и от изображения точки до оси. Эти перпедикуляры будем считать высотами точки и её изображения:
h - высота точки
Н - высота изображения
По формуле линейного увеличения линзы выясним отношение Н к h:
Г = Н/h
Из свойств подобных треугольников следует, что отношение стороны одного из них к такой же стороне другого треугольника равно отношению двух других сторон треугольников. H и h - это противолежащие катеты двух прямоугольных треугольников А'В'О и АВО, а f и d - их прилежащие катеты, f - расстояние от изображения точки до линзы, d - расстояние от точки до линзы. Поэтому:
Г = H/h = f/d
Найдём f по формуле тонкой линзы:
1/f + 1/d = 1/F
1/f = 1/F - 1/d = (d - F)/Fd
f = Fd/(d - F)
Подставим это выражение в формулу увеличения линзы:
Г = Н/h = f/d = (Fd/(d - F)) : d = Fd/((d - F)d) = F/(d - F)
Выразим высоту изображения точки:
Г = Н/h => H = hГ = Fh/(d - F)
Если двигать линзу вверх-вниз, то отношение высот Н и h не поменяется, т.е. формула линейного увеличения линзы будет работать и после её перемещения вниз на Δs. Точка остаётся на месте, но относительно линзы, а значит относительно и оптической оси, она перемещается на такое же расстояние Δs, только вверх. А расстояние от точки до оси - это перпендикуляр, который мы условились считать высотой h. Следовательно новая высота h' после перемещения линзы равна:
h' = h + Δs
Подставим это в формулу для Г':
Г' = Г = H'/h' = H'/(h + Δs) = F/(d - F)
Выражаем H':
H' = (h + Δs)*F/(d - F) = (Fh + FΔs)/(d - F)
Расстояние ΔS, на которое переместится изображение точки на экране, равно изменению высоты изображения:
ΔS = ΔH = H' - Н = ((Fh + FΔs)/(d - F)) - (Fh/(d - F)) = (Fh + FΔs - Fh)/(d - F) = FΔs/(d - F) = 4*3/(12 - 4) = 12/8 = 3/2 = 1,5 см
ответ: на 1,5 см.
Дано:
v = 340 м/с
t = 3 с
s - ?
s = v ⋅ t / 2 = 340 ⋅ 3 / 2 = 510 м