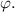 Поперечная к петле сила, действующая на кабинку, складывается из силы нормальной реакции и тяжести:
Поперечная к петле сила, действующая на кабинку, складывается из силы нормальной реакции и тяжести: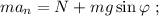
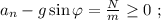
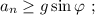
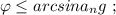
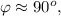 т.е. в самой верхней точке, то отрыв не произойдёт ни в одной точке.
т.е. в самой верхней точке, то отрыв не произойдёт ни в одной точке.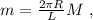 где
где 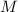 – масса всей сцепки.
– масса всей сцепки.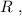 а значит, потенциальная энергия возрастёт по сравнению с горизонтальным участком на:
а значит, потенциальная энергия возрастёт по сравнению с горизонтальным участком на: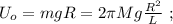
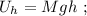
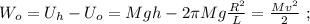
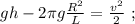
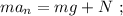
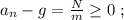
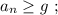
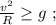
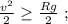
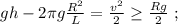
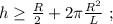
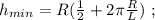
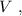
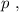
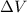 и
и 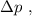
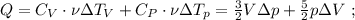
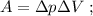
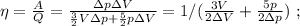
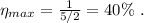
Объяснение:
S₀=a²; L=4*a - периметр (длина рамки)
S₀=a²=0,3²м²=0,09м²
1) L=2πR; R=L/(2π)=4*a/(2π)=2*a/π; S₁=πR²=π*(2*a/π)²=4*a²/π=0,1146м²
2) L=(x+2x)*2=6x; x=L/6=4*a/6=2*a/3; 2x = 4a/3; S₂=x*2x=8*a²/9=0,08м²
3) L=(0+y)*2; y=2a; S₃=0*y=0
Ф=B*S*cos(α); cos(α)=1=const; B=const
U=dФ/dt=B*dS/dt
I=U/R=B/R*dS/dt
q=integral (I*dt) = integral (B/R*dS/dt*dt) = integral (B/R*dS) =B/R*ΔS
1) q₁ = B/R*ΔS₁=B/R*(S₁ -S₀) = ( 1 Тл ) / (1 Ом) * (0,1146м² -0,09м²)=0,0246 Кл
2) q₂ = B/R*ΔS₂=B/R*(S₂ -S₀) = ( 1 Тл ) / (1 Ом) * (0,08м² -0,09м²)= - 0,01 Кл
3) q₃ = B/R*ΔS₃=B/R*(S₃ -S₀) = ( 1 Тл ) / (1 Ом) * (0,0м² -0,09м²)= - 0,09 Кл