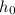Физика: На чем основана электрастатическая защита

На чем основана электрастатическая защита

👇

Увидеть ответ

Ответ:

nogtev70

13.03.2023

На экранировании. Окружить металлической сеткой. Внутри проводника эл. поля нет.

4,7(94 оценок)

Открыть все ответы

Ответ:

naziraa021

13.03.2023

Высоту "ватерлинии" поплавка относительно поверхности воды обозначим как y. Когда поплавок в равновесии, y=0, а когда всплывает, y>0. Пусть нижняя грань поплавка в состоянии равновесия находится на глубине h_0

. Тогда в процессе движения глубина погружения поплавка h=h_0-y

.
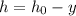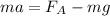На поплавок действуют сила тяжести, направленная вниз, и сила Архимеда, направленная вверх. Напишем уравнение движения по второму закону Ньютона: ma = F_A - mg

, где

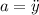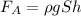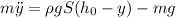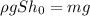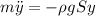- ускорение поплавка по вертикали, $a=\ddot{y}$ . Сила Архимеда равна весу воды вытесенной погруженной частью поплавка, т.е. $F_A=\rho gSh$ . Отсюда $m\ddot{y} = \rho gS(h_0-y) - mg$ . Так как в покое сила Архимеда и сила тяжести уравновешиваются, $\rho gSh_0 = mg$ , то $m\ddot{y} = -\rho gSy$ . Выражаем ускорение: 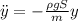$\ddot{y} = -\frac{\rho gS}{m}y$ . Это является уравнением колебаний с собственной частотой 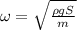$\omega = \sqrt{\frac{\rho gS}{m}}$ . 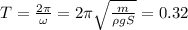Осюда период колебаний: $T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{\rho gS}}=0.32$ с.

4,8(72 оценок)

Ответ:

masha91672

13.03.2023

Варианты где последовательно в цепи включено одно из сопротивлений - исключаются, так как в этом случае общее сопротивление будет больше 2 Ом. Вариант, где все сопротивления включены параллельно, тоже исключается, так как в этом случае сопростивление цепи будет меньше наименьшего из сопротивлений, т.е. - меньше 2 Ом. Остаются три варианта когда два последовательно включенных сопротивления шунтируются третьим:
          R1          R2
   | ---|XXX|-----|XXX|---|
---|            R3          |---
   |----------|XXX|----------|
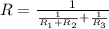Сопротивлении цепи в этом случае равно: $R = \frac{1}{\frac{1}{R_1+R_2}+\frac{1}{R_3}}$ . Методом перебора находим, что R=2 Ом, тогда, когда R1=2 Ом, R2=4 Ом, R3=3 Ом.
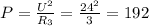Через сопротивление 4 Ом течет тот же ток, что и через сопр. 2 Ом, так как они включены последовательно. Напряжение, приложенное к обоим этим сопротивлениям будет: U=4А*(2Ом+4Ом)=24В. К сопр. 3 Ом приложено то же напряжение, значит мощность рассеиваемая на этом сопр.: $P=\frac{U^2}{R_3} = \frac{24^2}{3} = 192$ Вт.