ПРОЕКЦИЯ СИЛЫ ТЯЖЕСТИ, ДЕЙСТВУЮЩЕЙ НА ДОСКУ ВДОЛЬ НАКЛОННОЙ ПЛОСКОСТИ, РАВНА М G SIN А. СЛЕДОВАТЕЛЬНО, ПРИ РАВНОВЕСИИ ДОСКИ ТАКАЯ ЖЕ СИЛА ДОЛЖНА ДЕЙСТВОВАТЬ НА ДОСКУ В ПРОТИВОПОЛОЖНОМ НАПРАВЛЕНИИ СО СТОРОНЫ ЧЕЛОВЕКА. ПО ТРЕТЬЕМУ ЗАКОНУ НЬЮТОНА НА ЧЕЛОВЕКА СО СТОРОНЫ ДОСКИ ТАКЖЕ БУДЕТ ДЕЙСТВОВАТЬ СИЛА РЕАКЦИИ, РАВНАЯ М G SIN А И НАПРАВЛЕННАЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ ВНИЗ (РИС. 234; ИЗОБРАЖЕНЫ ЛИШЬ ТЕ СОСТАВЛЯЮЩИЕ СИЛ, ДЕЙСТВУЮЩИХ НА ДОСКУ И ЧЕЛОВЕКА, КОТОРЫЕ НАПРАВЛЕНЫ ВДОЛЬ НАКЛОННОЙ ПЛОСКОСТИ). ПО ВТОРОМ ЗАКОНУ НЬЮТОНА УСКОРЕНИЕ ЧЕЛОВЕКА ВДОЛЬ НАКЛОННОЙ ПЛОСКОСТИ ОПРЕДЕЛЯЕТСЯ СУММОЙ ПРОЕКЦИЙ СИЛ ПО ЭТОМУ НАПРАВЛЕНИЮ: MА = = MG SIN А + М G SIN А. ИЗ ЭТОГО УРАВНЕНИЯ НАЙДЕМ, ЧТО ЧЕЛОВЕК ДОЛЖЕН БЕЖАТЬ С УСКОРЕНИЕМ А= GSIN A(1 + М/Т), НАПРАВЛЕННЫМ ВНИЗ. НАПРАВЛЕНИЕ ДВИЖЕНИЯ САМОГО ЧЕЛОВЕКА ПРИ ЭТОМ БЕЗРАЗЛИЧНО.
Объяснение:
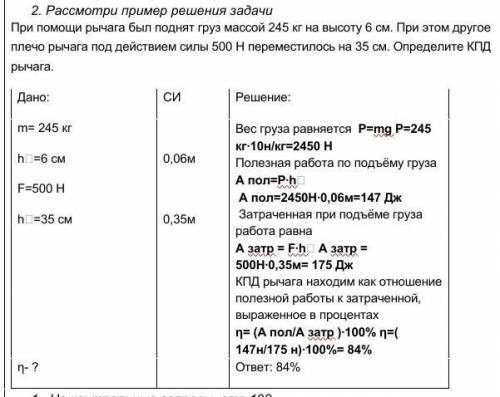
вроде правильно или нет
Честно говоря, я даже не представляю как здесь решить по-простому. В задаче многовато неизвестных, которые в одно-два действия и не выразишь.
Дано:
h = 5 см
H = 15 см
Δd = 1,5 см
H' = 10 см
F - ?
Линзу не меняли, значит мы можем приравнять выражения для отношения (1/F) друг к другу:
d' нам известно - оно равняется расстоянию до передвижения d + изменение расстояния Δd:
d' = d + Δd
Тогда выразим f и f' из формулы линейного увеличения линзы (вместо традиционной буквы "Г" я использую букву "G", поскольку редактор уравнений не может прописывать русские буквы):
Подставляем эти выражения в уравнение (1):
Получили значение первичного расстояния между свечой и линзой. Подставляем его в выражение для первичного расстояния f между экраном и линзой:
Возвращаемся к уравнению для обратного фокусного расстояния (1/F), переворачиваем его и подставляем найденные значения:
ответ: 9 см.