Дано:
q₁ = q₂ = q₃ = q₄ = Q = 10⁻⁷ Кл
Найти: q₀
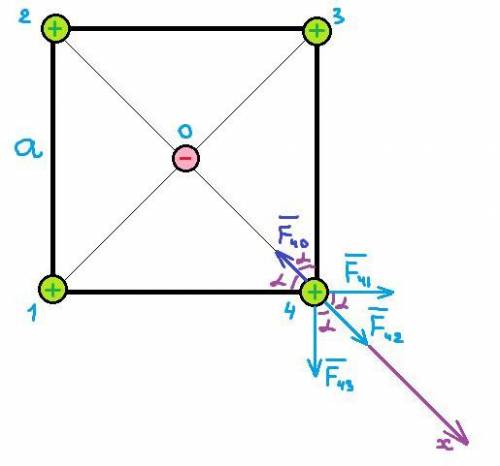
Изобразим графически все заряды. Заряды в вершинах квадрата пронумеруем от 1 до 4, заряду в центре квадрата присвоим номер 0.
Если система находится в равновесии, то векторная сумма сил, действующих на каждый из зарядов равна 0. Заметим, что поскольку картинка симметрична относительно центрального заряда, то выбирать его для рассмотрения смысла нет. Выберем для рассмотрения один из зарядов, расположенных в вершинах квадрата, например, № 4.
Запишем:
Введем ось, на которую спроецируем эти силы. Удобно направить эту ось вдоль диагонали квадрата. Тогда, получим:
Введенный угол 
, так как диагональ квадрата делит его на два равных равнобедренных прямоугольных треугольника.
Подставляя значение косинуса этого угла и расписывая силы Кулона, получим:
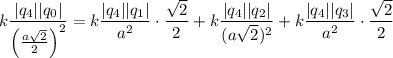
Величина 
соответствует стороне квадрата:
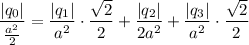
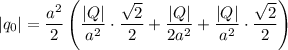
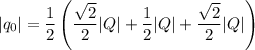
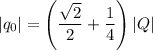
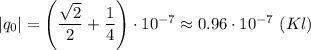
Так как искомый заряд отрицательный, то:
q₀ ≈ -0.96·10⁻⁷ Кл
ответ: -0.96·10⁻⁷ Кл
ответ:0,4
Объяснение:
Щоб пересунути по підлозі скриню масою 15 кг, до неї потрібно прикласти горизонтальну силу 60 Н. Знайдіть коефіцієнт тертя між скринею та підлогою, вважаючи, що g= 10 m/c².
Дано:
m=15кг
F=60H
g=10м/с2
Знайти: μ
Щоб пересунути скриню, треба діяти з силою, яка дорівнює силі тертя.
F=T
Сила тертя визначається формулою: T=μmg
де μ - коефіцієнт тертя.
μ=T\mg
З урахуванням рівняння можемо записати у вигляді
μ=F\mg
Підсттавимо дані у отриману формулу:
μ=60\15∗10=0,4
Відповідь: коефіцієнт тертя становить 0,4