Объяснение:
1)
Заменяем распределенную нагрузку сосредоточенной силой Q.
Точка приложения этой силы точка D - середина отрезка ЕС
Тогда:
CD = CE/2 = 1,2 /2 = 0,6 м
Q = q·EC = 4·1,2 = 4,8 кН
2)
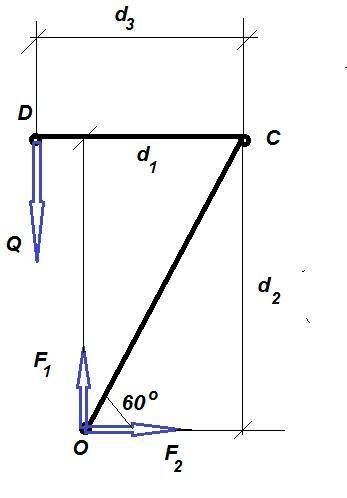
Реакцию жесткой заделки R заменим вертикальной и горизонтальной составляющей F₁ и F₂ (по теореме Вариньона).
F₁ = R·sin α = R·sin 60° ≈ 0,866·R
F₂ = R·cos α = R·cos 60° ≈ 0,5·R
3)
Сделаем чертеж.
d₃ = CD = 0,6 м
d₁ = OC·cos 60° = 1,8·0,5 = 0,9 м
d₂ = OC·sin 60° = 1,8·0,866 ≈ 1,6 м
Составляем уравнение моментов относительно точки С:
∑ Mc = 0;
Q·d₃ - F₁·d₁ + F₂·d₂ = 0
4,8·0,6 - 0,866·R·0,9 + 0,5·R·1,6 = 0
2,88 - 0,78·R + 0,8·R = 0
0,02R = - 2,88
R = - 2,88 / 0,02 = - 144 кН
Знак "-" говорит о том, что стержень СЖАТ!
1) 1,78 г
2) 19726 В/м
3) 1,44 м
Объяснение:
Задача 1. Сделаем рисунок с указанием всех сил.
Условие равновесия системы имеет вид
В проекциях на координатные оси
Выразим силу натяжения нити Т через кулоновскую силу отталкивания и найдем массу шарика
Кулоновскую силу можно найти как произведение величины заряда на поле бесконечной заряженной плоскости, коей является стена
Окончательно (конечно переведя заряд в СИ)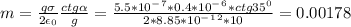 кг или 1,78 г.
кг или 1,78 г.
Задача 2.
Найдем сначала расстояние от вершин до центра квадрата, для этого распишем потенциал поля как сумму потенциалов отдельных зарядов
Откуда
Согласно принципу суперпозиции, напряженности полей, даваемые противоположными зарядами
Так как угол между ними прямой, для нахождения результирующего заряда воспользуемся теоремой Пифагора
Задача 3.
Найдем скорость иона перед влетом в поле
Найдем индукцию поля
Сила Лоренца сообщает иону центростремительное ускорение, из этих соображений найдем радиус траектории