

Объяснение:
Задача 1
Дано:
Vo = 1,5 м/с - скорость пловца относительно воды (относительная)
Vе = 0,5 v/c - скорость течения реки (переносная)
____________
Va - ? - абсолютная скорость относительно берега.
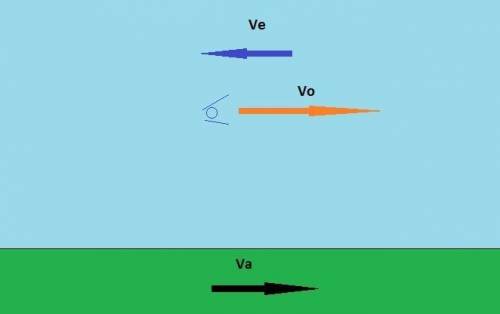
Решим задачу с векторов.
Абсолютная скорость тела равна векторной сумме относительной и переносной скоростей:
Vа = Vo + Ve
Сделаем чертеж (смотри приложение)
Из чертежа следует:
Va = Vo - Ve = 1,5 - 0,5 = 1 м/с
Задача 2
Дано:
V₁ = 72 км/ч = 20 м/с - скорость автомобиля
V₂ = 10 м/с = скорость автобуса.
___________
V отн - ?
Скорость "сближения" автомобилей
ΔV = V₁-V₂ = 20 - 10 = 10 м/с
1)
Считаем автомобиль неподвижным, тогда скорость автобуса равна "минус 10 м/с" (автобус как бы движется навстречу стоящему автомобилю).
2)
Считаем автобус неподвижным, тогда скорость автомобиля равна "плюс 10 м/с" (автомобиль приближается к стоящему автобусу).
Любое тело 5 метров пролетает за 1 секунду.
Составляем уравнение времени полёта второго камня.
Обозначим за V скорость его бросания вверх.
Время подъёма до верхней точки t₁ = V/g
Высота подъёма h равна: h = V²/2g.
Путь падения равен высоте подъёма плюс 8-5 = 3 м.
Время падения второго камня равно:
t₂ = √((2h + 3)/g) = √((2(V²/2g)+3)/g).
Сумма t₁ и t₂ равна 1 секунде.
(V/g) + (√((2(V²/2g)+3)/g)) = 1.
Первое слагаемое перенесём направо, возведём в квадрат и приведём к общему знаменателю.
2V² + 12g = 2g² - 4gV + 2V².
Подставив g = 10 м/с², получим V = 80/40 = 2 м/с.