1) При параллельном соединении проводников (смотри на прикреплённом рисунке):
- 1/R= 1/R1 + 1/R2+1/R3..., либо по другому R=(R1*R2*R3..)/(R1+R2+R3..) ;
- U везде одинаковое U = U1 = U2 = U3...;
- i (ток) i = i1 + i2 + i3...
2) При последовательном соединении проводников (смотри на прикреплённом рисунке):
- R= R1 + R2+R3... ;
- U = U1 + U2 +U3 +...;
- i (ток) i = i1 = i2= i3 ...
3) Рисунки приложил ниже
4) Показание амперметра = 0,1 А
Показание вольтметра V2 = 2 В
5) Показание амперметра А1 = 1,2 А
Показание амперметра А2 = 0,4 А
R2 = 300 Ом
Объяснение:
Задача №4.
Ток в цепи везде одинаковый, значит узнав ток через R1 , мы узнаем и ток через R2 (они при соединении последовательно ОДИНАКОВЫ).
R1 = 30 Ом U1 = 3В,
По закону Ома i = 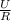
Подставляем:
i = 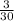 =
= 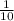 = 0,1 А
= 0,1 А
То есть ток протекающий во ВСЕЙ цепи равен 0,1 А. Этот ток 0,1 А пробегает и через R1 и через R2 , он одинаков во всей цепи (соединение последовательное).
Теперь можно узнать напряжение на R2.
R2 = 20 Ом , i = 0,1 А
По закону Ома i = 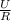 , U = i * R
, U = i * R
Подставляем:
U2 = 0,1 А * 20 Ом = 2 В
Задача №5
Сила тока при параллельном соединении =
i = i1 + i2
Амперметр А1 покажет силу тока i1 , а амперметр А2 покажет силу тока i2 .
ПО закону Ома узнаём какой ток будет бежать через R1:
По закону Ома i = 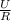
R1 = 100 Ом U1 = 120В,
Подставляем:
i1 =  = 1,2 А
= 1,2 А
ОБЩИЙ ток = i = i1 + i2 у нас известные i = 1,6 А , i1 = 1,2 А
i2 = i - i1
Подставляем:
i2 = 1,6А - 1,2 А = 0,4 А
Теперь определяем СОПРОТИВЛЕНИЕ R2.
По закону Ома i = 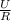 , либо R =
, либо R = 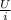
Подставляем:
R2 = 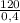 = 300 Ом
= 300 Ом
З власного досвіду ви знаєте, що у воді підняти камінь значно легше, ніж коли він лежить на березі, тому що у воді на до приходить виштовхувальна сила.
Закон, за яким можна розраховувати виштовхувальну силу, що діє на занурене в рідину тіло, відкрив давньогрецький вчений Архімед.
Тому виштовхувальну силу часто називають силою Архімеда (FA).
Сила Архімеда зумовлена тим, що тиск рідини збільшується з глибиною (на нижню поверхню зануреного в рідину тіла рідина тисне з більшою силою, ніж на верхню, унаслідок цього рівнодійна сил тиску рідини на всі ділянки поверхні тіла напрямлена вгору - ця рівнодійна і є силою Архімеда).
Унаслідок занурення у воду тіла, підвішеного до пружинних ваг, їх покази зменшаться завдяки виштовхувальній силі: коли кажуть, що занурене у воду тіло «втрачає у вазі», насправді, звичайно, ніякої «втрати у вазі» немає (вага тіла, що перебуває у спокої, завжди дорівнює силі тяжіння), але внаслідок занурення тіла у воду (часткового або повного) вага тіла перерозподіляється між підвісом — вагами і опорою — водою (тому показ ваг дорівнює різниці між вагою тіла та модулем виштовхувальної сили). Тільки із цим застереженням можна умовно назвати показ ваг «вагою тіла у воді». Це так зване гідростатичне зважування, його можна застосовувати, коли густина тіла більша за густину рідини, щоб тіло тонуло у рідині (визначити відношення густини тіла до густини рідини за формулою , це співвідношення дозволяє знайти N3густину тіла, якщо відома густина рідини, або знайти густину рідини, якщо відома густина тіла).
Спочатку з’ясуємо, чому на будь-яке тіло, занурене в рідину, діє сила Архімеда. Тиск у кожній точці рідини передається однаково в усіх напрямках і залежить від глибини. Розглянемо сили тиску, які діють у рідині на всі поверхні зануреного в неї тіла.
Нехай тіло має форму прямокутного паралелепіпеда На верхню грань тіла діє тиск p1 = рр ghl стовпчика рідини висотою h1. Сила тиску на цю поверхню з боку рідини становить F1 = p1S = рр gh1S де рр — густина рідини; S — площа поверхні тіла. Ця сила направлена вертикально вниз.
Тиск рідини на бічні грані змінюється з глибиною. Але на одному й тому самому рівні він однаковий. Тому сили тиску F, які діють на бічні поверхні, однакові й протилежно направлені, а їх рівнодійна дорівнює 0.
Нижня поверхня знаходиться на глибині h2. Її площа така сама, як і верхньої грані. На нижню поверхню тіла діє сила F2 = p2S = рр gh2S, яка направлена вертикально вгору. Оскільки нижня поверхня знаходиться глибше ніж верхня (h2 > h1), а їх площі однакові, то сила F2 більша за силу F1. Їх рівнодійна дорівнює різниці цих сил і направлена вгору. Рівнодійна сил тиску рідини на нижню та верхню грані тіла і є тією результуючою силою, що виштовхує (або намагається виштовхнути) тіло з рідини:
FA = F2 – F1 = p2S - p1S = рр gh2S - рр gh1S = ρрg(h2 — h1)S = ρрg Vт
Як видно з мал. h2 — h1 = h — висота прямокутного паралелепіпеда, а (h2 — h1) S = Vт — його об’єм. Остаточно можна записати, що
Альтернативные источники энергии – это приборы , устройства, или сооружения, позволяющие получать электрическую энергию (или другой требуемый вид энергии) и заменяющие собой традиционные источники энергии, функционирующие на нефти, добываемом природном газе и угле.
К таким источникам энергии относят: энергию Солнца, ветра, тепла Земли, энергию морей и океана, биомассу, новые виды жидкого и газообразного топлива, представленные синтетической нефтью на основе угля, органической составляющей горючих сланцев и битуминозных пород, а также некоторые виды топливных спиртов и водород.
Многие из нетрадиционных источников энергии являются сложными энергоресурсами, компоненты которых позволяют получать и нетопливную продукцию, широко применяемую в химии, строительной индустрии, сельском хозяйстве, металлургии и т.д.
Основное преимущество альтернативных источников энергии является неисчерпаемость и экологическая чистота. Их использование не изменяет экологический баланс планеты. Такие источники энергии играют значительную роль в решении трех глобальных проблем, стоящих перед человечеством: энергетики, экологии, продовольствия.
1.2. Солнечная энергетика
Солнце как источник энергии
Солнце является основным источником всех видов энергии, которыми человек имеет в своем распоряжении. Этот резервуар неисчерпаем. Достаточно сказать, что в течение 1,1*109 лет Солнце израсходует всего лишь около 2% аккумулированной в нём энергии.
Наша Земля, находясь в среднем на расстоянии 149 млн.км от Солнца, не получает и половины одной миллионной доли потока энергии излучаемой Солнцем. Кроме того, в среднем около 40% этой падающей энергии отражается на границе земной атмосферы обратно в межзвездное пространство. Тем не менее общее количество лучистой энергии, достигающее поверхности Земли в области суши, составляет за год 9,5*1017 кВт/ч. Это огромное количество энергии, непрерывно приходящее на поверхность Земли от Солнца в течение года, в 32 000 раз больше той энергии, которая поступает за это время в мировую энергетическую систему от разных источников энергии, таких, как минеральное топливо, гидроэнергия и пр.
История развития.
Пращурами, отцами солнечной энергетики на нашей планете следует считать французского физика Александра Эдмона Беккереля, электрика-изобретателя из Нью-Йорка Чарльза Фриттса, а также знаменитого Альберта Эйнштейна, обладателя Нобелевской премии. Первый, ещё в 1839 году заметил фотоэффект, представляющий собой излучение электронов под воздействием солнечного света. Второй, 44 года спустя, создал первый солнечный модуль — покрытый тонким слоем золота селен. КПД этой первой солнечной батареи был весьма низок — около 1%. Но это был первый шаг. В 1905 году Эйнштейн получает Нобелевскую премию как раз за доработку идей Беккереля. В 30-х годах века отечественные учёные под руководством академика А.Ф. Иоффе создали первые солнечные сернисто-таллиевые элементы. КПД их тоже был низок. Однако работы над солнечными батареями продолжились. В начале 50-х годов ХХ века, в США, в лаборатории компании Bell Telephone, Джеральд Пирсон со товарищи установил, что кремний с определённым покрытием заметно более чувствителен к солнечному свету, чем селен. В итоге была создана солнечная ячейка-батарея с КПД около 6% — началась эра развития солнечных батарей.
В 1957 году в СССР был запущен первый искусственный спутник с применением фотогальванических элементов, а в 1958 г. США произвели запуск искусственного спутника Explorer-1 с солнечными панелями. С 1958 года кремниевые солнечные батареи стали основным источником энергии для космических кораблей и орбитальных станций. Во время нефтяного кризиса 1973-74 гг. сразу несколько стран запустили программы по использованию фотоэлементов, что привело к установке и опробованию свыше 3100 фотоэлектрических систем только в Соединенных Штатах. Многие из них до сих пор находятся в эксплуатации.
Очередной всплеск интереса к солнечной энергетике пришелся на нефтяной кризис 1973–1974 годов, когда многие страны лихорадочно бросились искать альтернативные источники энергии. Только в США за это время было установлено более 3000 фотоэлектрических систем. Производились солнечные часы и калькуляторы, строились дома, использующие исключительно энергию солнца.
Первая попытка производства солнечной энергии в промышленных масштабах была предпринята в США, где в 1981 году заработала гелиотермальная электростанция в пустыне Мохаве. Ее площадь составляла 83 тысячи квадратных метров, а мощность – 10МВт. Удачный опыт ее использования дальнейшему развитию солнечной энергетики