решение смотри на прикрепленном изображении
______________________________
удачи!)
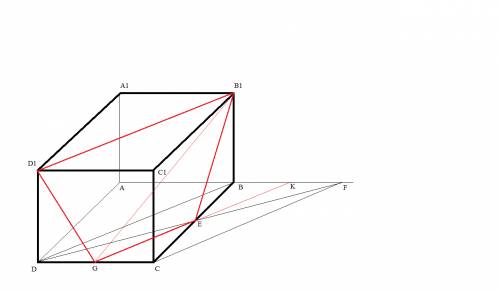
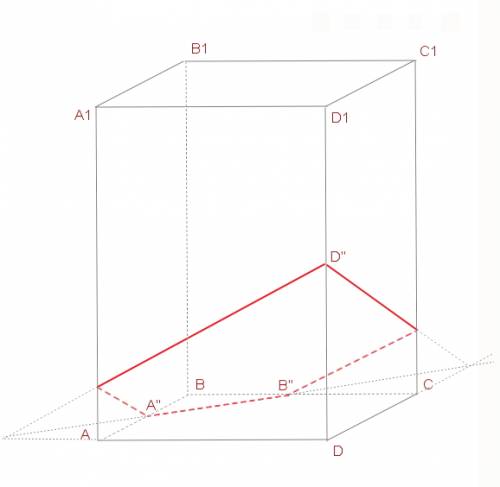
сделаем построение по условию
точка G - середина отрезка CD
точки B1, D1,G образуют плоскость GB1D1
дополнительные построения
прямая (BD) параллельна (B1D1)
прямая (CF) параллельна (BD)
прямая (GK) параллельна (BD)
прямая (CB) -секущая для параллельных прямых (BD) ,(GK), (CF)
по теореме Фалеса, прямая (CB) отсекает пропорциональные отрезки DG=GC и CE=EB
по теореме Пифагора
GE^2 = GC^2+CE^2=(D1C1/2)^2+(B1C1/2)^2 =( (D1C1)^2+(B1C1)^2 )/4 = (B1D1)^2 / 4
GE = B1D1/2 - отрезки GE и B1D1 НЕ РАВНЫ
прямая (GK) параллельна (BD) , а значит и (B1D1) и проходит через точку G в плоскости GB1D1
следовательно прямая (GK) принадлежит плоскости GB1D1
точка E - пересечение (GK) и (CB)
точки Е и B1, а значит и отрезок EB1 принадлежат плоскости GB1D1
искомое сечение - четырехугольник GD1B1E ,
противоположные стороны B1D1 и EG параллельны и не равны.
Основной признак ТРАПЕЦИИ:
четырёхугольник является трапецией, если его параллельные стороны не равны.
ДОКАЗАНО
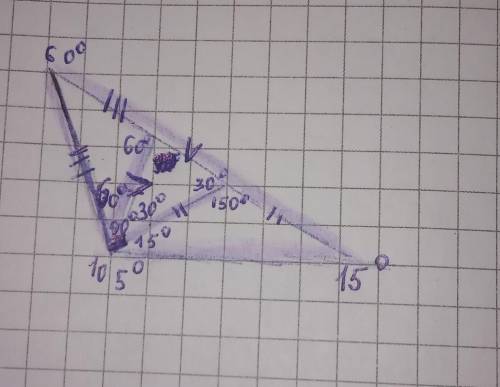
пусть данный треугольник АВС, АВ>ВС>СА. угол АСВ=105, угол АВС=15, угол ВАС=60. разделим СВ пополам (точка Д) и востановим из этой точки перпендикуляр до пересечения с АВ (точка К) , проведем отрезок КА. треугольник ВКС - равнобедренный с углами у основания 15 град. построим дугу с центром в точке А и проходящую через точку С до пересечения с АВ (точка М) треугольник АМС равнобедренный и равносторонний с углом 60 град. но и треугольник СМК тоже равнобедренный, т. к. угол МКС=углу КСМ=30 град, а угол КМС=120 град. это легко устанавливается из своиств углов треугольников (сумма их равна 180 град) и своиства открытого угла