Объяснение:
m ⁷₃Li = 7,01601 а.е.м.
m ²₁d = 2,0141 а.е.м.
m ⁴₂He = 4,0026 а.е.м.
Q = ? мэв
Решение
⁷₃Li + ²₁d ---> 2 ⁴₂He + Q
При грубом приближении масса частиц до реакции больше, чем после:
(7 + 2) > 4 * 2.
Значит, у продуктов реакции больше, чем у исходных ядер, кинетическая энергия и данная ядерная реакция не была эндоэнергетической, а, наоборот, экзоэнергетическая (с повышением энергии) и можно писать + Q
Для точного вычисления энергетического выхода через дефект масс надо знать массы ядер, т.е. из данных в условии масс надо вычесть массы электронов: me = 0,000548 а.е.м.
масса ядра изотопа лития : m( ⁷₃Li ) = 7,01601 - 3*0,000548 = 7,01601 - 0,001644 = 7,014366 а.е.м.
масса ядра гелия (α-частицы) : m (⁴₂He ) = 4,0026 - 2*0,000548 = 4,0026 - 0,001096 = 4,001504
дефицит массы: 7,014366 + 2,0141 - 2*4,001504 = 9,028466 - 8,003008 = 1,025458
энергетический выход: Q = 931,5Δm = 931,5 * 1,025458 ≈ 955,2 МэВ
ответ: 955,2 МэВ
Примечание: 955,2 МэВ -это очень большая энергия. Возможно, в условии что-то не учтено?
0,02 Н*с/м
Объяснение:
На шарик действуют две силы - сила тяжести, направленная вниз и сила сопротивления воздуха, направленная вверх. Второй закон Ньютона в проекции на ось y запишется в виде
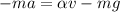
Или, в дифференциальной форме
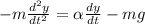
Однако ускорение 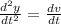 , значит
, значит
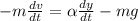
Поместим правую часть под знак дифференциала
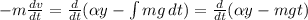
Перенесем все в левую часть
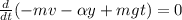
Значит выражение в скобках является постоянной величиной
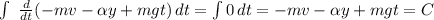
Константу интегрирования найдем из начальных условий 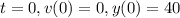
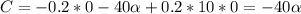
Значит
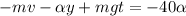
Рассмотрим теперь конечное состояние тела (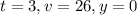 ), подставив все это в полученное уравнение найдем коэффициент сопротивления (знак минус возник из-за не совсем правильного выбора направления оси у, на самом деле ось надо было направить вниз, поэтому просто возьмем значение по модулю, решение было проверено через точное решение дифференциального уравнения но эти выкладки здесь будут излишними ввиду их громоздкости и сложности)
), подставив все это в полученное уравнение найдем коэффициент сопротивления (знак минус возник из-за не совсем правильного выбора направления оси у, на самом деле ось надо было направить вниз, поэтому просто возьмем значение по модулю, решение было проверено через точное решение дифференциального уравнения но эти выкладки здесь будут излишними ввиду их громоздкости и сложности)
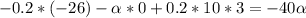
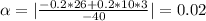 Н*с/м.
Н*с/м.
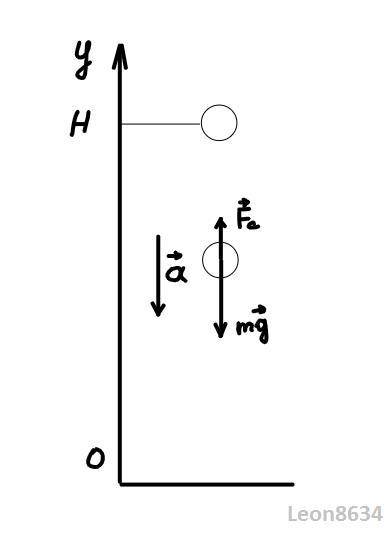
Импульс тела
p=m*V
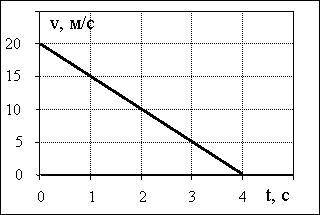
В момент t=2 c V(2)=10 м/с из графика
р=2 * 10=20 кг * м/с - это ответ. Или 20 Н/с. Это одно и тоже.