
1). Условие равновесия рычага:
F₁L₁ = F₂L₂ => F₂ = F₁L₁ : L₂ = m₁gL₁ : L₂ = 15·10·3 : 6 = 75 (H)
2). Наклонная плоскость дает выигрыш в силе во столько раз, во сколько ее длина больше высоты.
Таким образом, выигрыш в силе будет минимальным при максимальном наклоне плоскости к горизонту, то есть у второй плоскости с углом наклона 42°.
3). В том случае, если синий груз обозначен m₁, красный - m₂,
зеленый - m₃:
Условие равновесия рычага:
F₁L₁ + F₂L₂ = F₃L₃
m₁gL₁ + m₂gL₂ = m₃gL₃
m₂ = (m₃gL₃ - m₁gL₁) : gL₂ = (64·10·3 - 15·10·4) : (10·2) = 66 (кг)
4). Если грузы слева направо обозначены: m₁; m₂; m₃; m₄, то:
Условие равновесия левого рычага:
m₁gL₁ = m₂gL₂ => m₂ = m₁gL₁ : gL₂ = 80·2 : 1 = 160 (кг)
Общая масса левого рычага: m' = 80 + 160 = 240 (кг)
Условие равновесия нижнего рычага:
m'gL₁ = m''gL₂ => m'' = m'L₁ : L₂ = 240·1 : 5 = 48 (кг)
Условие равновесия правого рычага:
m₃gL₃ = m₄gL₄
Так как m₃ + m₄ = m'' = 48 (кг), то:
(48 - m₄)L₃ = m₄L₄
48 - m₄ = m₄ · 3
4m₄ = 48
m₄ = 12 (кг) m₃ = 48 - 12 = 36 (кг)
Для начала найдем расстояние, пройденное грузовым автомобилем от точки А до второго автомобиля. Так как встретились машины в 13:16, а грузовой автомобиль выехал в 12:00, найдем время, за которое он проехал от 12:00 до 13:16:
t₁ = 13 ч. 16 мин. - 12 ч. = 796 мин. - 720 мин. = 76 мин.
Найдем расстояние по формуле S = vt:
S₁ = 75 км/ч. * 76 мин. = 1,25 км/мин. * 76 мин. = 95 км.
Теперь найдем расстояние, пройденное легковым автомобилем от точки А до грузового автомобиля. По той же схеме находим время, затраченное на дорогу:
t₂ = 13 ч. 16 мин. - 12 ч. 10 мин. = 796 мин. - 730 мин. = 66 мин.
Далее найдем расстояние по той же формуле:
S₂ = 80 км/ч. * 66 мин. = 80 км/ч. * 1,1 ч. = 88 км.
Теперь сложим эти расстояния и получим расстояние от города А до города В:
S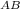 = S₁ + S₂ = 95 км. + 88 км. = 183 км.
= S₁ + S₂ = 95 км. + 88 км. = 183 км.
ответ: 183 км.