2.3 Момент инерции системы точек вычисляется по формуле: 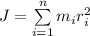 , где
, где 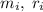 - соответственно масса i-той точки и расстояние от i-той точки до оси.
- соответственно масса i-той точки и расстояние от i-той точки до оси.
Для начального положения: 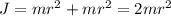 ; для конечного:
; для конечного: 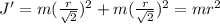 ; Получили, что момент инерции системы уменьшился в два раза.
; Получили, что момент инерции системы уменьшился в два раза.
2.2 Так как зависимость параболическая, то 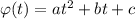 ;
;
Заметим, что коэффициент c - есть ордината точки пересечения параболы с осью OY (действительно, чтобы в этом убедиться достаточно подставить x=0).
Координаты вершины также достаточно просто вычислить. Имеем: 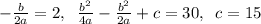 ; Отсюда легко вывести, что
; Отсюда легко вывести, что 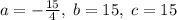 ; Итак,
; Итак, 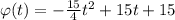 , значит,
, значит, 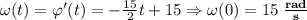
Далее постулаты, следуют из второго закона термодинамики:
Постулат Клаузиуса.
Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких либо других изменений в системе. Это явление называют рассеиванием или дисперсией энергии.
Постулат Кельвина.
Процесс, при котором работа переходит в теплоту без каких либо других изменений в системе, является необратимым, то есть невозможно превратить в работу всю теплоту, взятую от источника с однородной температурой, не проводя других изменений в системе.