173,2кН
Объяснение:
По сути говоря можно провести условную ось центральную, относительно которой два троса будут симместричны(относительно оси).
В таком случае решение сводится к разложению сил на координаты(параллельно тросу пусть будет x. перпендикулярно соответственно y). Используя тригонометрию можем вычислить косинус одного из тросов и соответственно умножить на 2.
Т.к. угол общий между тросами 60 градусов, следовательно из-за разбиения сего угла на две части каждый трос относительно оси будет под углом 30 градусов.
cos30=0.866
Можно найти одну силу и умножить на два, получаем: 100кН*2(силы)*0,866=173,2 кН
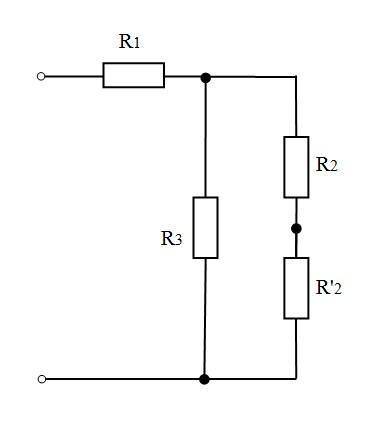
Схема состоит из:
группы сопротивлений R₂ и R₂', соединенных последовательно,
сопротивления R₃, соединенного параллельно с первой группой,
сопротивления R₁, соединенного последовательно с первыми двумя группами.
Преобразовать схему можно так: (см. рис.1)
Тогда общее сопротивление R₂ и R₂':
R₂₂ = R₂ + R₂' = 20 + 20 = 40 (Ом)
То есть сопротивления R₂ и R₂' можно заменить одним сопротивлением R₂₂ = 40 (Ом) (см. рис.2)
Общее сопротивление R₂₂ и R₃:
R₂₂₃ = R₂₂•R₃ : (R₂₂+R₃) = 40•60 : 100 = 24 (Ом)
Общее сопротивление цепи с учетом R₁:
R = R₁ + R₂₂₃ = 6 + 24 = 30 (Ом)
Общий ток в цепи:
I = I₁ = U/R = 240 : 30 = 8 (A)
Напряжение на первом сопротивлении:
U₁ = I · R₁ = 8 · 6 = 48 (B)
Напряжение на группе сопротивлений R₂₂₃:
U₂₂₃ = U - U₁ = 240 - 48 = 192 (B)
Ток, протекающий через R₃:
I₃ = U₂₂₃ : R₃ = 192 : 60 = 3,2 (A)
Ток, протекающий через R₂₂:
I₂₂ = U₂₂₃ : R₂₂ = 192 : 40 = 4,8 (A)
Напряжение на R₂ и R₂':
U₂ = U₂' = R₂I₂₂ = R₂'I₂₂ = 20 · 4,8 = 96 (B)
T1=400 K
P1=4*10^5 Па
V1=2*10^-3 м³
P'-?
1. Изотермический процесс, т.е. Т=соnst, P1*V1=Р2*V2
2.Изобарный процесс, P=const, V2/T1=V3/T2, T2=200K
3.Изотермический процесс, Т=сonst, P2*V3=P'*V4, V4=1*10^-3 м³
Тут нужно сделать систему и решить, подставляя. Я б решил, но тороплюсь. Удачи!