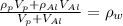. Обозначения: p - поплавок, w - вода, Al - проволока. Объем поплавка - площадь сечения цилиндра умножить на его высоту: 
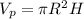. Объем проволоки - число витков умножить на длину витка умножить на площадь сечения проволки: 
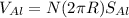. Подставив это в начальное уравнение для плотностей и выразив число витков N, получим: 
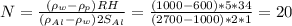витков. Заметьте, что мы перевели радиус и высоту поплавка в мм, чтобы привести произведение RH к единицам площади сечения проволоки.
E = (i/2)kT - средняя (!) энергия одной молекулы газа.
n = N/V => n*m = p - плотность, где m - масса одной (!) молекулы
E = mv²/2, где v - среднеквадратичная скорость.
Pm = pkT => (i/2)Pm = pE = p mv²/2 => (i/2)P = p v²/2
v² = iP/p
i - количество степеней свободы в газе.
Её значение, из условия задачи не следует. i = 3 для одноатомного, i = 5 для двуатомного и i = 6 для газа более чем из двух атомов. Эти числа верны для достаточно небольших температур.