Дано:
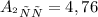 эВ
эВ
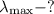
Согласно уравнению Эйнштейна для фотоэффекта энергия поглощенного кванта hν идет на совершение работы выхода A и на сообщение кинетической энергии вылетевшему электрону: 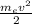
Работа выхода A - это минимальная работа, которую надо совершить, чтобы удалить электрон из металла.
Минимальная частота света v (min), при которой ещё возможен фотоэффект, соответствует максимальной длине волны λmax:

В этой формуле h – это постоянная Планка, равная 6,62·10-³⁴ Дж·с, частоту колебаний можно выразить через скорость света c, которая равна 3·108 м/с, и длину волны по формуле:
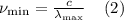
Подставим выражение (2) в формулу (1), тогда:
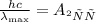
Откуда искомая красная граница фотоэффекта λmax равна:
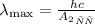
Посчитаем численный ответ (напоминаем, что 1 эВ = 1,6·10-¹⁹ Дж:
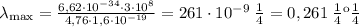
ответ: 0,261 мкм.
v0 = 3 м/с
а = 2 м/с²
Объяснение:
Мы знаем что
s = v0t + ( at² )/2
или
s = v0t + at²0,5
Зная это составим систему
s(1) = v0t(1) + at(1)²0,5
s(2) = v0t(2) + at(2)²0,5
Где а ; v0 постоянные постоянные величины ( ускорение и начальная скорость тела ( соответственно ) ) ( подставим численные значения и решим систему )
40 = v0 5 + a 5² * 0,5
130 = v0 10 + a 10² * 0,5
Упростим
40 = 5v0 + 12,5а
130 = 10v0 + 50a
Разделим обе части уравнения на 5
8 = v0 + 2,5a | * ( -2 )
26 = 2v0 + 10a
-16 = -2v0 - 5a
26 = 2v0 + 10a
Суммируем две системы уравнения ( и получим одно уравнение )
10 = 5a
отсюда
а = 2 м/с²
Подставим численное значение ускорения в уравнение 8 = v0 + 2,5a и решим относительно начальной скорости тела
8 = v0 + 5
отсюда
v0 = 3 м/с
m = 20 кг масса льда
С = 2100 Дж на кг на град - удельная теплоёмкость льда
λ = 330 000 Дж на кг - удельная теплота плавления льда
ΔT = 20 C - нагрев льда с -20 до точки плавления (0 с)
Q = 20(2100*20 + 330 000) = 7440000 Дж