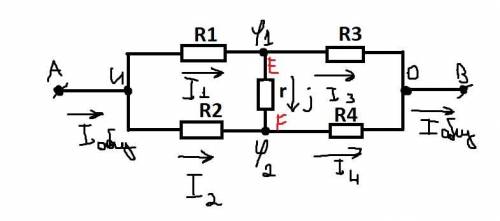
Мост Уитстона является сбалансированным когда разность потенциалов равна нулю, по нашей схеме если φ1-φ2=0, то мост Уитстона в нашем случае является сбалансированным.
В узел E, поступает ток I1 и из узла выпускает ток I3 и j, ток j=0, так как напряжение - это разность потенциалов, а у нас в этом месте φ1-φ2=0 то есть как раз разность потенциалов равна нулю (так как это сбалансированный мост Уитстона) значит и напряжение на этом участке равно 0 и по закону Ома j=U/r где r-сопротивление резистора; j-ток протекающий через этот участок; U-разность потенциалов на этом участке. Следовательно j=0/r даже не зная r понятно, что j=0 А так как 0 в числителе. Поэтому по закону сохранения заряда какой ток поступает в узел такой и выпускает. То есть I1=I3+j мы выяснили что j=0, следовательно I1=I3.
В узел F, поступает ток j и I2, а выпускается ток I4. По закону сохранения заряда j+I2=I4 так как мы выяснили, что j=0, то I2=I4.
Так как φ1-φ2=0, то φ1=φ2 обозначим их как просто φ, то есть φ1=φ2=φ.
Так как напряжение - это разность потенциалов (по определению), то по закону Ома:
I1=(U-φ1)/R1=(U-φ)/R1
I3=(φ1-0)/R3=(φ-0)/R3=φ/R3
I2=(U-φ2)/R2=(U-φ)/R2
I4=(φ2-0)/R4=(φ-0)/R4=φ/R4
Раз I1=I3 и I2=I4, то:
1) I1=I3
(U-φ)/R1=φ/R3
2) I2=I4
(U-φ)/R2=φ/R4
Составим систему уравнений:
(U-φ)/R1=φ/R3
(U-φ)/R2=φ/R4
(U-φ)/φ=R1/R3
(U-φ)/φ=R2/R4
Следовательно:
R1/R3=R2/R4
R1*R4=R2*R3 - это значит, что когда у нас сбалансированный мост Уитстона, то произведения сопротивлений по диагонали равны.
Каждое равенство R1*R4=R2*R3 - это 1 комбинация (1 отдельный сбалансированный мост Уитстона), главное чтобы в каждой комбинации были разные R1 и R2 и R3 и R4 (так как по условию просят, чтобы резисторы, а следовательно и сопротивление было разным).
Также следим чтобы во всех комбинациях не повторялись цифры больше чем 5 раз, так как по условию у нас имеется по 5 штук резисторов каждого сопротивления от 1 Ом до 10 Ом.
Ну и само собой R1, R2, R3, R4 не может быть меньше 1 Ом и больше 10 Ом (по условию).
Я нашёл таких комбинаций 8 штук, вот они:
1) 1*10=2*5
2) 1*8=2*4
3) 1*6=2*3
4) 2*6=3*4
5) 2*10=4*5
6) 3*8=4*6
7) 3*10=5*6
8) 4*10=5*8
То есть итого можно собрать одновременно из этого набора как максимум 8 сбалансированных мостов Уитстона, при том что в каждой мостовой схеме все резисторы имеют разное сопротивление.
ответ: Можно собрать одновременно из этого набора как максимум 8 сбалансированных мостов Уитстона, при том что в каждой мостовой схеме все резисторы имеют разное сопротивление.Объяснение:
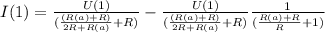
1. Т. к амперметр неидеален, то его можно заменить его резистором c сопротивлением:
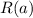- сопротивление амперметра
2. Далее по известным школьным методам расчета общего сопротивления можно найти общее сопротивление всей электрической цепи:
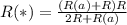
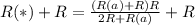
3. В этой электрической цепи идет ток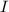 
, можно воспользоваться вторым правилом Кирхгофа, или же законом Ома для полной электрической цепи:
Правило Кирхгофа:
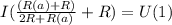
По закону Ома для полной электрической цепи:
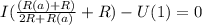
4. Выражаем ток:
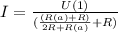
И в зависомости от сопротивлений на резисторах можно выразить ток.
Это общий ток, нам нужно найти ток черз амперметр, тогда можно сказать что 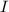состоит из двух токов:
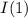- ток через амперметр
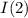- ток через верхнюю ветку
5. Т. к ток обратно пропорционально зависит от сопротивления, тогда:
Пусть через верхнюю ветку идет ток:
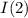, тогда через амперметр идет ток:
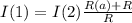
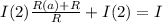
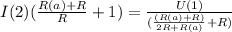
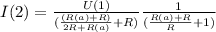
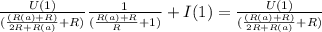
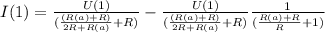
от мучений, если сам посчитаешь.)))
Запишем условие теплового равновесия:
Qв=Qл1 + Qл2 + Qл3 , где Qв - телота выделившаяся при охлождении воды, Qл1 - теплота, затраченная на нагрев льда до 0 С, Qл2 - теплота, затраченная на плавление льда, Qл3 - тело затраченное на нагрев воды, которая получилось после тачния льда.
1) Qв = Cв*Mв*(tв - tк) , где Св = 4200 дж/(кг*С), tв = +15C, tк - температура смеси
2) Qл1= Сл*Mл*(0C - tл), где Сл = 2100 дж/(кг*С), tл = -10С, 0С - это ноль градусов
3) Qл2 = Yл*Mл , где Yл = 340000 дж/кг
4) Qл3 = Св* Mл* (tк - 0С)
=> Cв*Mв*(tв - tк) = Сл*Mл*(0C - tл) + Yл*Mл + Св* Mл* (tк - 0С)
отсюда tк = (Св* Mв*tв + Сл*Mл*tл - Yл*Mл) / (Св* Mл + Cв*Mв)
т.к. Mв = M л = 0.5 кг, то
tк = (Св*tв + Сл*tл - Yл) / 2Св = -35 С.
Но т.к. такого быть не могло, то значит, что лед растаял не полностью и сследовательно вода и лед находятся при нуде градусов.
ответ: температура смеси = 0 С