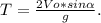
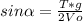
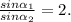
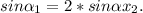
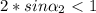
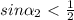
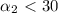 °
°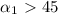
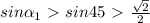
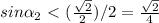
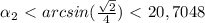 °.
°.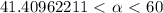
F qE q[VB]
эм
. (5.4)
Это выражение называется формулой Лоренца. Скорость
V
в этой формуле есть
скорость заряда относительно магнитного поля.
Для вывода общих закономерностей будем считать, что магнитное поле однородно,
а электрические поля на частицы не действуют.
При движении частицы со скоростью
V
вдоль линий магнитной индукции
B
магнитное поле не влияет на ее движение, так как модуль силы
F
равен нулю (см.
формулу (5.3)).
Если частица движется со скоростью
V
перпендикулярно к магнитному полю
B ,
то cила Лоренца, равная
F q V B m
, постоянна по модулю
F qVB m
и нормальна к
траектории частицы. Согласно второму закону Ньютона, эта сила создает ускорение:
F ma . Вектор полного ускорения
a равен векторной сумме нормального и
тангенциального ускорений:
n a a a
. Тангенциальное ускорение
a
, характеризующее
изменение модуля скорости от времени, равно нулю, т.е.
0
dV
a
dt
, поскольку модуль
скорости не изменяется во времени (о чем сказано выше). Следовательно, сила Лоренца
создает центростремительное (нормальное) ускорение
2 V
r
. Отсюда следует, что частица
будет двигаться по окружности, радиус которой определяется из условия
Объяснение: думаю так
время полета пропорционально вертикальной составляющей скорости
имеем 2 уравнения
sin(2*a)=sin(2*b)
sin(a)=2*sin(b)
sin(a)*cos(a)=sin(b)*cos(b)
sin(a)=2*sin(b)
2*cos(a)=cos(b)
sin(a)=2*sin(b)
2*cos(a)=cos(b)
sin(a)/2=sin(b)
(2*cos(a))^2+(sin(a)/2)^2=1
4*(cos(a))^2+(sin(a))^2/4 =1
4*(1-sin(a))^2)+(sin(a))^2/4 =1
3=(sin(a))^2*15/4
4/5=(sin(a))^2
sin(a)=корень(0,8)
а = arcsin(корень(0,8)) = 63,43495 градус