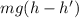. Внутренняя энегрия идеального двухатомного газа по формуле равна 
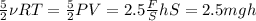. Тут я использую то, что давление газа изнутри компенсирует давление поршня. Значит, изначальная энергия системы равна 
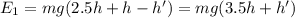. После остановки движения энергия груза станет равна 0, а внутренняя энергия газа станет равна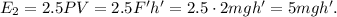 
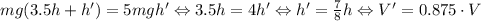= 3.5 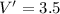л.
л
Потенциальная энергия всегда считается относительно какого-то уровня, который принят за ноль. Вот например если за ноль принять уровень пола 3го этажа, то на втором этаже потенциальная энергия очевидно отрицательна.