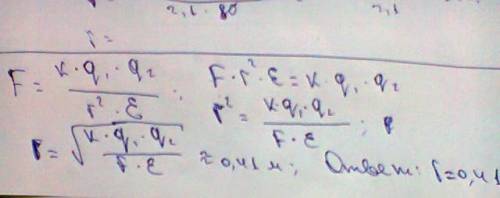
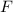к краю.
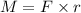, где 
- расстояние от оси вращения то точки приложения силы. Оказывается, момент силы прямо пропорционален угловому ускорению двери! Чем больше момент, тем сильнее дверь ускоряется. будет наибольшим. Сила в 3 Н приложенная на 1 м от оси создает такой же момент, как и сила в 6 Н, приложенная на расстоянии 0.5 м. Чем дальше от оси мы прикладываем силу, тем легче нам вращать дверь. Для ручки в середине двери момент будет меньше, чем если ручка находится у края. Попробуй открыть дверь, прикладывая силу очень близко к петлям. Трудно? Вот тут и оно.
Дано:
d = 10 см = 0,10 м
σ = 2 мкКл = 2·10⁻⁶ Кл/м²
L = 12 см = 0,12 м
E - ?
x = (d + L) = 0,10+0,12 = 0,22 м - расстояние от центра цилиндра до заданной точки
Воспользуемся формулой вычисления напряженности, созданной заряженным цилиндром:
E = σ·d / (2·ε₀·x)
E = 2·10⁻⁶·0,10 / (2·8,85·10⁻¹²·0,22) ≈ 51 400 В/м или 51,4 кВ/м