векторы скорости лодки и мальчика составляют прямой угол.
у лодки и мальчика - взаимноперепндикулярные импульсы
надо сделать векторное сложение
скалярная сумма по теореме Пифагора
катет 1 = p1 =m1v1 = 100*1=100 кг/*м/с
катет 2 = p2 =m2v2 = 50*2= 100 кг/*м/с
гипотенуза p12 = √(p1^2+p2^2)=√2*100^2=100√2 кг/*м/с
p12 = (m1+m2)u
u = p12 / (m1+m2) = 100√2 /(100+50) = 2√2/3 = 0.94 м/с
направление движения <A между берегом и новым направлением лодки
cosA =p1/p12 =100 /100√2 = 1/√2 =√2 /2
<A=45 град
ОТВЕТ 0.94 м/с ; направление ее движения 45 град
Так.
Дано:
m=1 кг.
P1=8 Н.
P2=6 Н.
p=? (Плотность раствора).
p1=1000 кг/м^3. (Плотность воды).
_______
Решение:
Мы знаем формулу для силы тяжести, запишем ее:
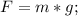
Считаем для нашего случая:
F=1*10=10 Н.
Теперь, запишем формулу для веса тела, исходя из условия задачи: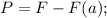
Где F(a) - Архимедова сила, формула которой: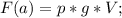
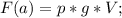
Где p - плотность жидкости, g - ускорение свободного падения, V - Объем тела.
Запишем формулу для веса тела в первом случае: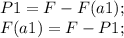
Получаем:
F(a1)=10-8=2 Н.
Теперь расписав Архимедову силу найдем объем бруска: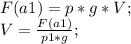
Считаем:
V=2/(1000*10)=0,0002 м^3.
Теперь запишем формулу веса тела для второго случая, расписав Архимедову силу. Выразим p:
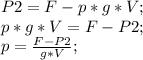
Считаем:
p=(10-6)/0,002=2000 кг/м^3.
ответ: p=2000 кг/м^3. Плотность раствора.
В вашем случае среднее арифметическое скоростей вычисляется так:
(15+х+х) /3=20, где х - условная средняя скорость велосипедиста во второй и в третьей третях пути.
Из уравнения мы видим, что х=(20*3-15)/2=22,5 км/ч.