Дано:
====================
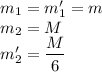
Найти: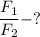 
====================
Решение. Сила всемирного тяготения — это сила, которая обуславливает притяжение всех тел во Вселенной. Она определяется законом всемирного тяготения, если тела можно принять за материальные точки или шары с однородным или радиальным распределением плотности (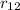
— расстояние между центрами масс взаимодействующих тел).
Закон всемирного тяготения, открытый Ньютоном: две материальные точки притягиваются одна к другой с силами, модуль которых прямо пропорциональный произведению их масс и обратно пропорциональный квадрату расстояния между ними:
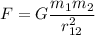
Итак, определим силы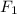 
и 
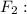
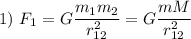
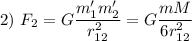
Зная силы, определим, во сколько раз одна больше другой:
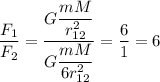или 
====================
ответ: сила взаимного притяжения тел уменьшится в 6 раз.
задания движения точки
Чтобы задать движение точки, надо задать ее положение по отношению к выбранной системе отсчета в любой момент времени. Для этого задания можно применять один из трех естественный, координатный, векторный.
1. Естественный задания движения точки
Естественным задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным.
Пусть точка движется относительно системы отсчета вдоль некоторой траектории (рис. 40). Выберем на этой траектории какую-нибудь неподвижную точку , которую примем за начало отсчета, а затем, рассматривая траекторию как координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси.
39
Тогда положение точки на траектории будет однозначно определяться криволинейной координатой , равной расстоянию от точки до точки , измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка будет перемещаться вдоль траектории, следовательно, расстояние будет с течением времени изменяться. Чтобы определить положение точки на траектории в любой момент времени, надо знать зависимость вида:
. (13)
Это уравнение выражает закон движения точки. Таким образом, чтобы задать движение точки естественным необходимо знать:
1. Траекторию движения точки;
2. Начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета;
3. Закон движения точки вдоль траектории .
Следует отметить, что величина определяет положение точки, а не пройденный ей путь. Например, если точка, двигаясь из начала отсчета, доходит до положения , а затем, двигаясь в обратном направлении, приходит в положение , то в этот момент ее координата , а пройденный за это время путь будет равен.
2.Координатный задания движения точки
В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде
, ,.(14)
При координатном задания движения точки траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами , которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.
Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную , получаем два уравнения движения,.
Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории.
При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).
40
Положение точки в этом случае будут определять полярными координатами и, т.е. уравнения движения точки вполярных координатах имеют вид .
Переход металла в жидкое состояние при нагревании его до температуры плавления
Мы знаем, что в кристаллах молекулы (или атомы) расположены в строгом порядке. Однако и в кристаллах они находятся в тепловом движении (колеблются). При нагревании тела средняя скорость движения молекул возрастает. Следовательно, возрастает и их средняя кинетическая энергия и температура. На графике это участок АВ (см. рис. 18). Вследствие этого размах колебаний молекул (или атомов) увеличивается. Когда тело нагреется до температуры плавления, то нарушится порядок в расположении частиц в кристаллах. Кристаллы теряют свою форму. Вещество плавится, переходя из твёрдого состояния в жидкое.
Следовательно, вся энергия, которую получает кристаллическое тело после того, как оно уже нагрето до температуры плавления, расходуется на разрушение кристалла. В связи с этим температура тела перестаёт повышаться. На графике (см. рис. 18) это участок ВС.
Опыты показывают, что для превращения различных кристаллических веществ одной и той же массы в жидкость при температуре плавления требуется разное количество теплоты.
Физическая величина, показывающая, какое количество теплоты необходимо сообщить кристаллическому телу массой 1 кг, чтобы при температуре плавления полностью перевести его в жидкое состояние, называется удельной теплотой плавления.
Удельную теплоту плавления обозначают λ (греч. буква «лямбда»). Её единица — 1 Дж / кг.
Определяют удельную теплоту плавления на опыте. Так, было установлено, что удельная теплота плавления льда равна 3,4 • 105 — . Это означает, что для превращения куска льда массой 1 кг, взятого при 0 °С, в воду такой же температуры требуется затратить 3,4 • 105 Дж энергии. А чтобы расплавить брусок из свинца массой 1 кг, взятого при его температуре плавления, потребуется затратить 2,5 • 104 Дж энергии.
Следовательно, при температуре плавления внутренняя энергия вещества в жидком состоянии больше внутренней энергии такой же массы вещества в твёрдом состоянии.
Чтобы вычислить количество теплоты Q, необходимое для плавления кристаллического тела массой т, взятого при его температуре плавления и нормальном атмосферном давлении, нужно удельную теплоту плавления λ умножить на массу тела m:
Q = λm.
Из этой формулы можно определить, что
λ = Q / m, m = Q / λ
Опыты показывают, что при отвердевании кристаллического вещества выделяется точно такое же количество теплоты, которое поглощается при его плавлении. Так, при отвердевании воды массой 1 кг при температуре 0 °С выделяется количество теплоты, равное 3,4 • 105 Дж. Точно такое же количество теплоты требуется и для плавления льда массой 1 кг при температуре 0 °С.
Превращение льда в воду
При отвердевании вещества всё происходит в обратном порядке. Скорость, а значит, и средняя кинетическая энергия молекул в охлаждённом расплавленном веществе уменьшаются. Силы притяжения теперь могут удерживать медленно движущиеся молекулы друг около друга. Вследствие этого расположение частиц становится упорядоченным — образуется кристалл. Выделяющаяся при кристаллизации энергия расходуется на поддержание постоянной температуры. На графике это участок EF (см. рис. 18).
Кристаллизация облегчается, если в жидкости с самого начала присутствуют какие-либо посторонние частицы, например пылинки. Они становятся центрами кристаллизации. В обычных условиях в жидкости имеется множество центров кристаллизации, около которых и происходит образование кристалликов.
Таблица 4.
Удельная теплота плавления некоторых веществ (при нормальном атмосферном давлении)
При кристаллизации происходит выделение энергии и передача её окружающим телам.
Количество теплоты, выделяющееся при кристаллизации тела массой т, определяется также по формуле
Q = λm.
Внутренняя энергия тела при этом уменьшается.
Пример. Для приготовления чая турист положил в котелок лёд массой 2 кг, имеющий температуру 0 °С. Какое количество теплоты необходимо для превращения этого льда в кипяток при температуре 100 °С? Энергию, израсходованную на нагревание котелка, не учитывать.
Нагревание льда в котелке
Какое количество теплоты понадобилось бы, если вместо льда турист взял из проруби воду той же массы при той же температуре?
Запишем условие задачи и решим её.