Определение
Силу натяжения определяют как равнодействующую сил (
ˉ
R
), приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто
ˉ
F
и
ˉ
T
, и
ˉ
N
. Математически определение для силы натяжения нити можно записать как:
ˉ
T
=−
ˉ
R
(1)
где
ˉ
R
= векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Объяснение:
100000000 працент
Объяснение:
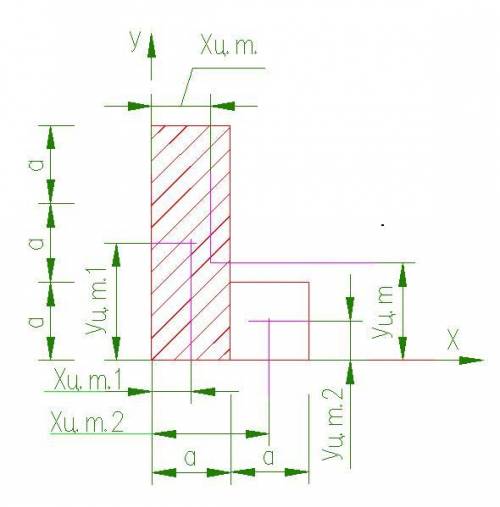
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
2. v=at a=v/t=30/20=1.5 м/сек² Fтяги-Fсопр=ma Fсопр=kmg
Fтяги=ma+kmg=m(a+kg)=1000(1.5+0.005*10)=1550 н
3. kx²/2=mgh k*0.2²/2=0.02*10*40 k*0.02=0.02*400 k=400 н/м
4. m1*g*x1=m2*g*x2 x1/x2=m2/m1=0.4/0.25=1.6
x1=1.6x2 x1+x2=52 x1=52-x2 1.6x2=52-x2 2.6*x2=52 x2=20 см
x1=52-20=32см