57,5 см
Объяснение:
Закон Архимеда:
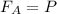, где сила Архимеда 
, ρ₁ - плотность воды, V₁ - объем погруженной части
тела, P - вес тела.
Для одной льдины закон Архимеда:
(1) 
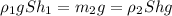, здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2) 
см
Для льдины с медным кубиком:
(3) 
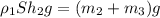, m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4) 
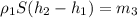, где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
, m₂ - масса льда, m₄ - масса железного кубика, H - глубина погружения льдины в воду с установленным железным кубиком.
Подставляем сюда выражение 1:
(5) 
.
Выразим массу железного кубика через массу медного:
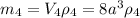, a - длина ребра куба, ρ₄ - плотность железа.
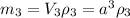, тогда:
(6) 
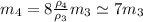
Подставляя (6), (4) в (5):
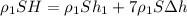
Упрощая это выражение и подставляя из (2) значение h₁:
см.
рассмотрим 1 удар
до удара
потенц энергия Еп=mgh
кинет энергия Ек =mv^2/2
по закону сохранения энергии равны Еп=Ек ; mgh =mv^2/2 ; gh =v^2/2 (1)
после удара
потенц энергия Еп1=mgh1
кинет энергия Ек1 =mv1^2/2
по закону сохранения энергии равны Еп1=Ек1 ; mgh1 =mv1^2/2 ; gh1 =v1^2/2 (2)
разделим (1) на (2)
gh / gh1=v^2/2 / v1^2/2
h / h1=v^2 / v1^2
h1 = h (v1/v)^2 считать постоянным, коэффициент восстановления k
h1 = h k^2 (3)
рассмотрим 2 удар
до удара
потенц энергия Еп1=mgh1
кинет энергия Ек1 =mv1^2/2
по закону сохранения энергии равны Еп1=Ек1 ; mgh1 =mv1^2/2 ; gh1 =v1^2/2 (4)
после удара
потенц энергия Еп2=mgh2
кинет энергия Ек2 =mv2^2/2
по закону сохранения энергии равны Еп2=Ек2 ; mgh2 =mv2^2/2 ; gh2 =v2^2/2 (5)
разделим (4) на (5)
gh1 / gh2=v1^2/2 / v2^2/2
h1 / h2=v1^1 / v2^2
h2 = h1 (v2/v1)^2 считать постоянным, коэффициент восстановления k
h2 = h1 k^2 подставим из (3) значение h1 = h k^2
h2 = h k^2 * k^2 = h* ( k^2 )^2 (6)
и так далее
после n -го удара уравнение (6) имеет вид
h(n)= h* ( k^2 )^n = h*k^(2n)
