Будем проводить эксперимент с водой, а не кофе, ибо вода доступнее. И кофе, и вода - жидкости, сделанные выводы будут касаться обеих жидкостей.
Вообще, нужно понимать, почему вода остывает. Уясним себе один факт - постоянный теплообмен. Сформулирую закон попроще: всё в мире, что касается друг друга, постоянно пытается достичь одинаковой температуры.
Итак, раз мы знаем факт теплообмена, нетрудно догадаться, почему вода остывает: она пытается достичь одной температуры с тем, с чем контактирует - с воздухом в комнате.
Нам понадобятся:
1) Термометр, рассчитанный до 100°C
2) Два одинаковых цилиндрических стакана
3) Линейка
Поехали! :)
Вместо объёма мы будем пользоваться высотой, ибо объём и высота прямо пропорциональны (V = S * h)
1) Наливаем горячую воду из под крана в первый стакан. Мерим температуру воды T01 термометром и высоту воды h1 в стакане линейкой.
3) Приложив линейку ко второму стакану, наливаем горячую воду высотой в два раза ниже, чем в предыдущем стакане:
h2 = h1 / 2.
Температура приблизительно та же, что и в первом, T02 = T01.
4) Ждём 5 минут, оставляя стаканы открытыми.
5) Ещё раз мерим температуру воды в стаканах, T1 и T2.
6) Считаем изменение температуры в первом стакане:
ΔT₁ = T₁ - T₀₁
И во втором стакане:
ΔT₂ = T₂ - T₀₂
7) Подставляем известные значения в формулу:
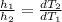
Равенство приблизительно сходится.
Вывод: чем больше объём жидкости, тем медленнее жидкость будет остывать.
Частота колебаний обратно пропорциональна периоду колебаний.
Общее уравнение гармонических колебаний
A = A(max)*sin(2(пи)*T + (фи))
где
A(max) - Амплитуда( максимальное значение отклонения)
Т - период колебания
(фи) начальная фаза колебания (относительное отклонение маятника, отклонение пружины от точки равновесия применительно к механическим моделям колебательных движений)
Приведем наличное отображение (уравнение в задаче) к каноническому виду
A(max) = 5
cos x = sin (x+ (pi)/2) = sin ((pi)/2*t/t(0) +(pi)/2) = sin((pi)/2*(t/t(0) +1)) или
2*(pi)*T = (pi)*t/2*t(0)
T = t*t(0)/4 откуда частота равна
f = 1/T = t*t(0)/4 = 0,25 Гц
Нам надо найти отношение w/v.
Первый раз Ахиллес догнал Черепаху, когда она м.
Ахиллес к этому моменту пробежал полный круг и еще x м, всего S+x м.
t1 = x/v = (S+x)/w
После встречи Ахиллес развернулся и побежал обратно. В момент второй встречи Черепаха оказалась в точке y м, то есть она м.
Ахиллес пробежал x м обратно до старта и еще S-y м до встречи.
Всего он пробежал S+x-y м.
t2 = (y-x)/v = (S+x-y)/w
Третий раз Черепаха закончила круг, S м. То есть м. Ахиллес развернулся и побежал туда же, что и Черепаха, причем обогнал ее со старта. Он пробежал S-y м до старта и еще круг, S м. Всего 2S-y м.
t3 = (S-y)/v = (2S-y)/w
Выразим w/v из всех трех уравнений
{ w/v = (S+x)/x
{ w/v = (S+x-y)/(y-x)
{ w/v = (2S-y)/(S-y)
Приравняем правые части этих уравнений
{ (S+x)/x = (S+x-y)/(y-x)
{ (S+x)/x = (2S-y)/(S-y)
Решаем пропорции
{ (y-x)(S+x) = x(S+x-y)
{ (S+x)(S-y) = x(2S-y)
Раскрываем скобки
{ Sy - Sx + xy - x^2 = Sx + x^2 - xy
{ S^2 + Sx - Sy - xy = 2Sx - xy
Приводим подобные
{ Sy - 2Sx = 2x^2 - 2xy
{ S^2 = Sx + Sy
Из 2 уравнения S = x + y. Подставляем в 1 уравнение
S(y - 2x) = 2x^2 - 2xy
(x + y)(y - 2x) = 2x^2 - 2xy
xy + y^2 - 2x^2 - 2xy = 2x^2 - 2xy
4x^2 - xy - y^2 = 0
Делим все на y^2
4(x/y)^2 - (x/y) - 1 = 0
D = 1 - 4*4*(-1) = 17
(x/y)1 = (1 - √17)/8 ≈ -0,39 - не может быть, x и y разных знаков.
(x/y)2 = (1 + √17)/8 ≈ 0,64 - подходит
x = y*(1+√17)/8; S = x + y = y*(1+√17)/8 + y = y*(9+√17)/8
Отношение скоростей Ахиллеса и Черепахи:
w/v = (S + x)/x = S/x + 1 = [y(9+√17)/8] : [y(1+√17)/8] + 1 =
= (9+√17)/(1+√17) + 1 = (9+√17)(√17-1)/(17-1) + 1 = (9√17+17-9-√17)/16 + 1 =
= (8√17+8)/16 + 1 = (1+√17)/2 + 1 = (1 + √17 + 2)/2 = (3+√17)/2 ≈ 3,56