Question

Пешеход стоит возле второго вагона поезда. поезд тронулся, пешеход заметил, что второй вагон проехал за 5 секунд. за какое время (с) пройдет десятый вагон мимо пешехода? движение считать равноускоренным. принять √8 = 2,82

Answer 1

Пусть S - длина одного вагона, t - время, за которое второй вагон проехал мимо пешехода, а tₓ - искомое время.

Формулы для равноускоренного движения:

$S = V_0t + \frac{at^2}{2}.$ (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)

$V = V_0 + at.$ (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)

Зная, что начальная скорость V₀ = 0, получаем:

$S = \frac{at^2}{2}, a = \frac{2S}{t^2}.$

$V = at = \frac{2S}{t}.$

Когда пешеход будет стоять у начала десятого вагона (назовём это момент 1, скорость в этот момент соответственно V₁), то возле него проедет уже 8 вагонов (с 2-ого по 9-ый), длина 8 вагонов S₁ = 8S.

Вспомним формулу не требующую наличие времени:

$S = \frac{V^2 - V_0^2}{2a}.$ (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ)

Для нашей задачи, учитывая, что V₀ = 0, формула имеет вид:

$S_1 = \frac{V_1^2}{2a}.$

Тогда отсюда скорость V₁

$V_1 = \sqrt{2aS_1} = \sqrt{2a*8S} = \sqrt{16aS} = 4\sqrt{\frac{2S^2}{t^2}} = 4\sqrt{2}\frac{S}{t}.$

Рассмотрим момент, когда пешеход будет стоять уже у конца 10-ого вагона (назовём это момент 2, скорость в этот момент соответственно V₂), тогда возле него проедет уже 9 вагонов, длина 9 вагонов S₂ = 9S.

Выразим скорость V₂:

$V_2 = \sqrt{2aS_2} = \sqrt{2a*9S} = 3\sqrt{2aS} = 3\sqrt{\frac{4S^2}{t^2}} = 6\frac{S}{t}.$

Используя формулу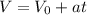 $V = V_0 + at$ (ВНИМАНИЕ! ФОРМУЛА В ОБЩЕМ ВИДЕ) для скоростей V₁ и V₂ найдём нужное нам время tₓ.

Формула примет следующий вид:

$V_2 = V_1 + at_x.$

Отсюда искомое время tₓ:

$t_x = \frac{V_2 - V_1}{a} = \frac{6\frac{S}{t} - 4\sqrt{2}\frac{S}{t}}{\frac{2S}{t^2}} = \frac{\frac{S}{t}(6-4\sqrt{2})}{2\frac{S}{t^2}} = \frac{t(6-2\sqrt{8})}{2}.$

Найдём окончательный численный ответ, подставив t = 5 с:

$t_x = \frac{5(6-2\sqrt{8})}{2} = 2,5 * (6 - 2 * 2,82) = 0,9$ (c).

Таким образом мы получили tₓ = 0,9 с.

ответ: 0,9 секунд.

Формулы "общего вида" своей символикой не имеют отношения к задаче, они просто выписаны в качестве "опоры".