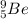По условию задачи дано:
Скорость движения автомобиля на скоростных участках: 100 км/ч
Скорость движения автомобиля на нескоростных участках: 50 км/ч
Время, за которое автомобиль должен доехать до пункта назначения: 6 часов
1) Для решения этой задачи нужно использовать формулу расстояния, скорости и времени:
Расстояние = Скорость * Время
Однако, на каждом из участков автомобиль двигался со своей скоростью. Для начала, нужно определить, сколько времени машина ехала со скоростью 100 км/ч.
Поскольку автомобиль должен был доехать до пункта назначения за 6 часов, а первые часы он двигался со скоростью 100 км/ч, значит, на скоростных участках он проехал 100 км/ч * 1 час = 100 км.
Таким образом, треть всего пути составляет 100 км.
Значит, на нескоростных участках автомобиль проехал 3 - треть всего пути, то есть 2/3 пути.
Так как на нескоростных участках автомобиль двигался со скоростью 50 км/ч, можно найти расстояние, которое он проехал на этих участках:
Расстояние = Скорость * Время
Расстояние = 50 км/ч * (2/3) * 6 часов
Расстояние = 50 км/ч * 4 часа = 200 км
Таким образом, на нескоростных участках автомобиль проехал 200 км.
Общее расстояние между Москвой и Псковом будет равно сумме расстояний на скоростных и нескоростных участках:
Расстояние = 100 км + 200 км = 300 км
Ответ: Расстояние между Москвой и Псковом составляет 300 км.
2) Чтобы найти среднюю скорость автомобиля на всем пути, нужно разделить общее расстояние на общее время.
Общее время = Время на скоростных участках + Время на нескоростных участках
Время на скоростных участках = 1 час
Время на нескоростных участках = 4 часа
Общее время = 1 час + 4 часа = 5 часов
Теперь мы можем найти среднюю скорость:
Средняя скорость = Общее расстояние / Общее время
Средняя скорость = 300 км / 5 часов
Средняя скорость = 60 км/ч
Ответ: Средняя скорость автомобиля при движении из Москвы в Псков составляет 60 км/ч.
Для решения данной задачи нужно использовать принцип Архимеда, который гласит: любое тело, погруженное в жидкость, испытывает со стороны этой жидкости вертикальную силу, равную весу вытесненной жидкости.
Шаг 1: Найдем объем вытесненной жидкости.
Объем кубика можно найти по формуле: V = a^3, где "a" - длина ребра куба.
V = 5^3 = 125 см^3
Для определения веса вытесненной жидкости воспользуемся формулой:
масса = плотность * объем.
масса жидкости = плотность воды * объем жидкости
масса жидкости = 1 г/см^3 * 125 см^3
масса жидкости = 125 г
Шаг 2: Найдем изменение объема надводной части кубика.
Для этого нужно найти 25% от объема кубика.
Изменение объема надводной части = 25% * объем кубика
Изменение объема надводной части = 0,25 * 125 см^3
Изменение объема надводной части = 31,25 см^3
Шаг 3: Найдем изменение массы вытесненной жидкости.
Для этого нужно найти 25% от массы вытесненной жидкости.
Изменение массы вытесненной жидкости = 25% * масса вытесненной жидкости
Изменение массы вытесненной жидкости = 0,25 * 125 г
Изменение массы вытесненной жидкости = 31,25 г
Шаг 4: Найдем вертикальную силу, которую нужно приложить к кубику.
По принципу Архимеда вертикальная сила равна весу вытесненной жидкости.
вес вытесненной жидкости = масса вытесненной жидкости * ускорение свободного падения (g)
г = 9,8 м/с^2
вес вытесненной жидкости = 31,25 г * 0,001 кг/г * 9,8 м/с^2
вес вытесненной жидкости = 0,30575 Н (округляем до 0,306 Н)
Ответ: Необходимо приложить вертикальную силу, равную 0,306 Н, чтобы объем надводной части кубика уменьшился на 25%.
Найдем количество протонов. Для этого разделим заряд ядра на элементарный заряд:
Количество протонов соответствует порядковому номеру в таблице Менделеева - это изотоп бериллия Be
Количество нуклонов А = Z + N,
где N- количество нейтронов
А = 4 + 5 = 9
Следовательно,