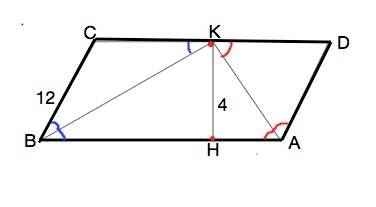
∠ КВС=∠КВА (ВК - биссектриса и делит ∠СВА пополам).
∠СКВ=∠КВА ( накрестлежащие при СD ║ ВА и секущей ВК).
∠СКВ=∠СВК, след. ∆ ВСК - равнобедренный и СК=ВС=12.
∠КАВ=∠КАD ( АК - биссектриса).
∠DКА=∠КАВ ( накрестлежащие).⇒ ∆ КDА - равнобедренный. КD=AD
В параллелограмме противоположные стороны равны.
След. AD=ВС=12 Сторона СD=12+12=24. Стонона АВ=CD=24
Расстояние между параллельными прямыми измеряется перпендикулярным к ним отрезком. КН - перпендикулярен АВ.
КН - высота АВСD.
Площадь параллелограмма находят произведением его высоты на сторону, к которой она проведена.
S=КН•AB=4•24=96 см²
Проекция апофемы A на основание в правильной треугольной пирамиде равна (1/3) высоты основания h.
(1/3)h = √(А² - Н²) = √(100 - 64) = √36 = 6.
Отсюда h = 3*6 = 18.
Сторона основания а = h/cos 30° = 18/(√3/2) = 12√3.
Периметр основания Р = 3а = 36√3
Площадь основания So = a²√3/4 = (144*3*√3)/4 = 108√3 кв.ед.
Площадь боковой поверхности равна:
Sбок = (1/2)АР = (1/2)*10*36√3 = 180√3 кв.ед.
Площадь полной поверхности S = 108√3 +180√3 = 288√3 кв.ед.