Рисунок во вложении, чтобы было понятнее. Поехали. У нас дан ромб, а ромб - параллелограмм, значит, у него противоположные углы равны >> угол D= угол В=150 градусов. Вычислим углы А и С: Угол А= угол С=180 - угол D=180 - угол B=30 градусов. Проведем высоту DH к AB. Катет ДН равен половине гипотенузы, так как он лежит против угла в 30 градусов(угла А), следовательно, ДН=3см. Проведем диагональ BD. Она разделит ромб на два равных треугольника(по трем сторонам, где диагональ - общая сторона). Значит, площади этих треугольников равны, а значит, площадь ромба будет равна удвоенной площади треугольника ABD. А площадь ABD мы можем найти, зная высоту и сторону, к которой эта сторона проведена. S(ABD)=0,5*AB*DH=0,5*6см*3см=4,5 см^2 Теперь умножаем на два эту площадь и получаем площадь ромба, равная 9 см^2 ответ:9см^2
Очень просто. Так как углы при основании равнобедренного треугольника равны, то углы, образованные биссектрисами этих углов, тоже будут равны, то есть: угол1=углу2=углу3=углу4 Так как угол2=углу 4, то треугольник AOC -равнобедренный, то есть АО=ОС. Рассмотрим теперь треугольники AOД и COE: -угол 1=углу 3, что мы доказали сначала -AO=OC, что мы доказали потом -угол AOД=углу COE как вертикальные Значит, треугольники AOC и COE равны по стороне и двум прилежащим ей углам >> OД=OE по равенству треугольников Так как: AE=AO+OE CD=СO+DE AO=CO OD=OE То AE=CD, чтд!
16√5
Объяснение:
AB=CD, значит трапеция равнобедренная.
Угол между высотой трапеции и CD равен ∠С-90°
sin(∠C-90) = -cos(∠C)=+2/3
Высота трапеции равна CD* cos(∠C-90)=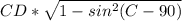 =
=
= 6*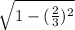 =
=
=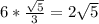
Половина разницы между основниями равна
CD*sin(∠C-90) = 6*(2/3)=4
Значит большее основание равно 4+2*4=12
Площадь трапеции равна (AD+BC)/2 * h = (4+12)/2 * 2√5 = 16√5