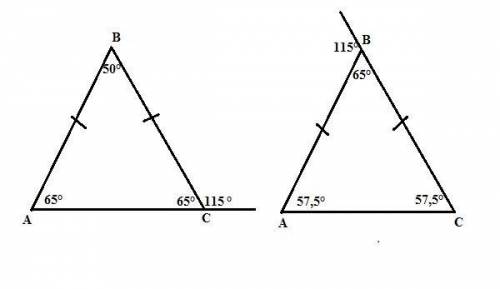
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
80° и 100°
Объяснение:
Сумма углов трапеции равна 360°
Мы имеем дело с равнобедренной трапецией, а у неё есть две пары одинаковых углов.
Пусть меньший угол равен x, тогда больший x + 20. Всего в трапеции 4 угла, то есть два малых и два больших
Составим уравнение:
x + x + x + 20 + x +20 = 360
4x + 40 = 360
4x = 360 - 40
4x = 320
x = 320 / 4
x = 80
Значит меньший угол равен 80°, тогда больший будет равен 80° + 20° = 100°
Удачи))