ответ: √(46/41)
Объяснение:
1. Поиск искомого отрезка
1) BM ⊂ (BSD)
AC ∩ (BSD) = O
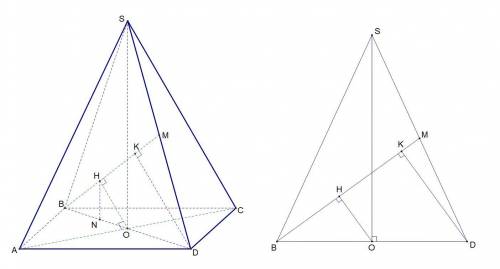
Проведём в ΔBMD из точки O перпендикуляр к BM
OH ⊥ BM
2) SO - высота пирамиды. Высота попадёт в точку O, так как пирамида правильная. SO ⊥ (BCD)
Проведём HN, HN || SO ⇒ HN ⊥ (BCD) ⇒ NO - проекция OH на (BCD)
3) HO - наклонная, NO - проекция, AC ⊂ (BCD) ⇒ HO ⊥ AC (по теореме о трёх перпендикулярах)
Таким образом, HO - общий перпендикуляр к прямым AC и BM ⇒ расстояние между AC и BM равно HO
2. Нахождение длины отрезка
HO ⊂ (BSD). Найдём HO из ΔBSD.
1) MD = SD/2 = 5/2
Из ΔABD по теореме Пифагора BD = 2√2, OD = BD/2 = √2 (св-во диаг. квадрата).
Тогда из ΔSOD cos∠SDO = OD/SD = √2/5
2) По теореме косинусов в ΔBMD имеем:
BM² = BD² + MD² - 2BD * MD * cos∠SDO
BM² = 8 + 25/4 - 10√2 * √2/5
BM² = 8 + 25/4 - 4
BM² = 41/4
BM = √41/2
3) sin∠SDO = √(1 - cos²∠SDO) = √(1 - 2/25) = √23/5
SΔBMD = 1/2 * MD * BD * sin∠SDO = 1/2 * 5/2 * 2√2 * √23/5 = √46/2
SΔBMD = 1/2 * BM * KD ⇒ KD = 2*SΔBMD : BM = 2*√46/2 : √41/2 = 2√46/√41
4) В ΔBKD OH || KD, BO = OD ⇒ HO - средняя линия ΔBKD ⇒ HO = KD/2 = √46/√41
1)Треугольник AOB равен тр-ку COD по 2 сторонам и углу между ними. Т.к они равны, то соотв. элем. равны. Угол OCD равен углу OBA - они накрест лежащие при прямых АВ и CD и сек. ВС. Следовательно, AB ║CD
2)Треугольники OXY и OZY равны по 3 сторонам. Т.к они равны, то соотв. элем. равны. Угол XOY равен углу YZO - они накрест лежащие при прямых OX и YZ и сек. OY. Следовательно, OX ║YZ. Также угол XYO = углу YOZ(из равенства тр-к) - они накрест лежащие при прямых OX и YZ и сек. OY. Следовательно, OZ ║XY
3)Треугольники ROB и SOT равны по стороне и двум прилежащим к ней углам. Т.к они равны, то соотв. элем. равны. Угол BRO = углу STO - они накрест лежащие при прямых RB и ST и сек. BS. Следовательно, RB ║ST. Также треугольники ROS и BOT равны по стороне и 2 прилежащим к ней углам. Отсюда угол SRO = углу BTO - они накрест лежащие при прямых RS и BT и сек. RT. Следовательно, RS ║BT.
1. чертим две прямые.далее с свойства смежных углов находим второй угол (180-22°) 180- так как сумма смежных углов равна 180°. Второй угол=158°. Пользуясь свойством вертикальных углов находим,что угол 3=углу 1=22°
угол 4=углу2=158°.