Sc = d²·tgα·√2/(2+tgα).
Sб = 4d²·tgα/(2+tgα).
So = d²/(2+tgα).
So =
Объяснение:
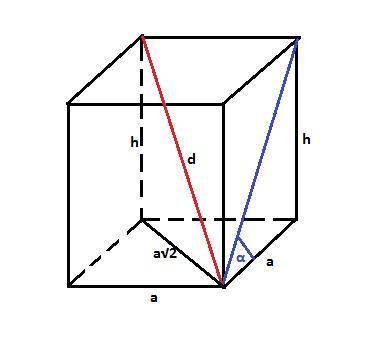
Призма правильная, значит в основании лежит квадрат. Пусть сторона квадрата равна "а". Тогда диагональ квадрата равна а√2.
Высота призмы равна h = a·tgα (из прямоугольного треугольника - половины боковой грани).
Квадрат диагонали призмы d² = h²+2a². (из прямоугольного треугольника - половины диагонального сечения).
d² = a²·tg²α+2a² = a²(2+tgα). => a = d/(√((2+tgα)).
h = a·tgα = d·tgα/(√((2+tgα)).
Тогда площадь диагонального сечения равна:
Sc = a√2·h = d√2/(√(2+tgα))·dtgα/(√(2+tgα)) = d²·tgα·√2/(2+tgα).
Площадь боковой поверхности равна произведению периметра основания на высоту призмы:
Sб = 4·a·h = 4d/(√((2+tgα))·d·tgα/(√((2+tgα)) = 4d²·tgα/(2+tgα).
Площадь основания (квадрата) равна квадрату стороны:
So = a² = d²/(2+tgα).
Расстояние равно √21/7.
Объяснение:
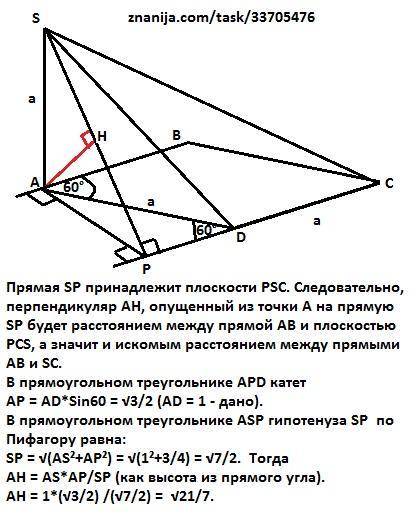
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Плоскость определяется двумя пересекающимися прямыми. В нашем случае плоскость DSC параллельна прямой АВ, так как прямая DC, принадлежащая этой плоскости, параллельна прямой АВ как прямые, содержащие противоположные стороны ромба.
Опустим перпендикуляр АР на прямую CD. АР перпендикулярна и прямой АВ. Соединим точки S и Р.
Прямая SP перпендикулярна прямой СР по теореме о трех перпендикулярах.
Прямая SP принадлежит плоскости PSC. Следовательно, перпендикуляр АН, опущенный из точки А на прямую SP будет расстоянием между прямой АВ и плоскостью PCS, а значит и искомым расстоянием между прямыми АВ и SC.
В прямоугольном треугольнике APD катет
АР = AD*Sin60 = √3/2 (AD = 1 - дано).
В прямоугольном треугольнике ASP гипотенуза SP по Пифагору равна: SP = √(AS²+AP²) = √(1²+3/4) = √7/2. Тогда
АH = AS*AP/SP (как высота из прямого угла прямоугольного треугольника).
АH = 1*(√3/2) /(√7/2) = √21/7.
Прямая MK и отрезок AC пересекаются, а точки их пересечения M.