60 ед.²
Объяснение:
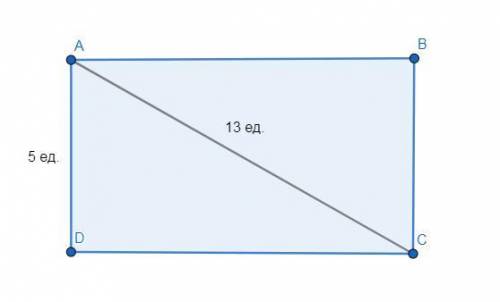
Рассмотрим ΔADC: ∠D = 90°, AD = 5 ед., AC = 13 ед.
Найдем DC, используя т. Пифагора (с² = а² + b², где с - гипотенуза, a,b - катеты)
13² = 5² + DC²
DC² = 13² - 5²
DC² = 169 - 25
DC² = 144
DC = 12 ед.
Найдем S прямоугольника по формуле: S = ab, где S - площадь, a,b - длина и ширина.
12 * 5 = 60 ед.² - S данного прямоугольника
60 (ед)²
Объяснение:
Рассмотрим ΔАВС - прямоугольный,
По т.Пифагора (для ΔАВС):
АC²=АB²+ВС²
13²=5²+ВС²
169=25+ВС²
ВС²=169-25
ВС²=144
ВС=√144
ВС=12
Sпрямоуг = AB*BC = 5 × 12 = 60 (ед)²