Если квадрат и ромб имеют одинаковые периметры, тто они имеют и одинаковые стороны. Воспользуемся следующей формулой для вычисления площади параллелограмма в случае ромба. В данном случае стороны равны, значит формула упрощается до . Заметим, что Это угол между сторонами ромба. Здесь не имеет значения острый или тупой, так как в обоих случаях будет положительный ответ. Площадь квадрата же всегда равна . Заметим, что синус всегда меняется в данном случае от 0 до 1. То есть только в случае синуса равного 1 (а это квадрат) площадь ромба равна площади квадрата, в остальных случаях площадь ромба всегда меньше площади квадрата.
Площадь параллелограмма равна произведению высоты на сторону
Для начала найдём другую сторону: в параллелограмме противоположные стороны равны, значит, периметр P=a+b+c+d=2a+2b=2(a+b) Мы знаем P=56 и a=10 Значит, 56=2(10+b) 56/2=10+b 28=10+b b=28-10=18 Вторая сторона равна 18 см Теперь найдём высоту: Рассмотрим ΔADH (рисунок ниже): Если это прямоугольный треугольник, и в нём угол 30°, то противоположный катет равен половине гипотенузы, т.е. HD=AD/2 AD = 10 см Значит, HD=5 см, то есть высота равна 5 см Теперь можно найти площадь: 18*5=60 см ответ: 60 квадратных сантиметров
Если квадрат и ромб имеют одинаковые периметры, тто они имеют и одинаковые стороны. Воспользуемся следующей формулой для вычисления площади параллелограмма в случае ромба.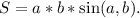
В данном случае стороны равны, значит формула упрощается до 
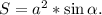. Заметим, что 
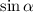Это угол между сторонами ромба. Здесь не имеет значения острый или тупой, так как в обоих случаях будет положительный ответ. Площадь квадрата же всегда равна 
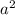. Заметим, что синус всегда меняется в данном случае от 0 до 1. То есть только в случае синуса равного 1 (а это квадрат) площадь ромба равна площади квадрата, в остальных случаях площадь ромба всегда меньше площади квадрата.