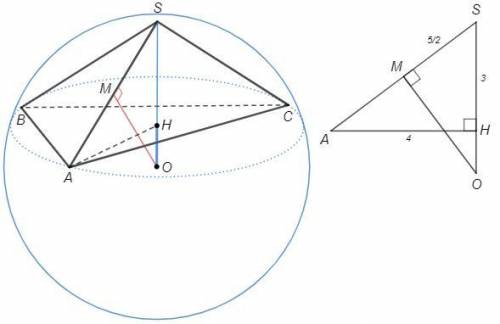
Основание ABC, AB=4, ∠C=30°
H - центр описанной окружности.
AB/sinC =2AH (т синусов) => AH=4
Если боковые ребра пирамиды равны, то вершина падает в центр описанной окружности основания.
SH⊥(ABC)
SH=√(SA^2-AH^2) =3 (т Пифагора)
О - центр описанной сферы.
OABC - пирамида с равными боковыми ребрами, следовательно ее вершина также падает в центр H.
OH⊥(ABC)
S-H-O на одной прямой.
В плоскости ASO.
OS=OA, О на серединном перпендикуляре к SA.
M - середина SA, SM=5/2
△SOM~△SAH
SO/SA=SM/SH => SO/5=5/2*3 => SO=25/6
OH =SO-SH =25/6 -3 =7/6
барсук Барчук Евгений барсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгенийбарсук Евгений
24; 8
Объяснение:
1) 16 * 2 = 32 - сумма двух основ
2) 32 : 4 = 8 - друга основа
3) 8 * 3 = 24 - перша основа