определить каноническое уравнение гиперболы, если угол между асимптотами равен 60 градусов и С= 2 корня из 3.
Угол между асимптотой и осью Ох равен 60/2 = 30 градусов.
Угловой её коэффициент или тангенс угла наклона к оси Ох равен
1/√3. Значит, в уравнениях асимптот у = +-(b/a)x значение b/a = 1/√3.
Отсюда находим соотношение a = b√3.
Далее используем заданное значение с = 2√3.
Так как с² = a² + b², то используем найденное соотношение a и b .
(2√3)² = (b√3)² + b²,
12 = 3b² + b²,
12 = 4b²,
b² = 12/4 = 3,
b = √3.
Тогда а = b√3 = √3*√3 = 3.
Найдены параметры a и b канонического уравнения параболы:
(x²/a²) - (y²/b²) = 1.
Подставляем найденные параметры и получаем
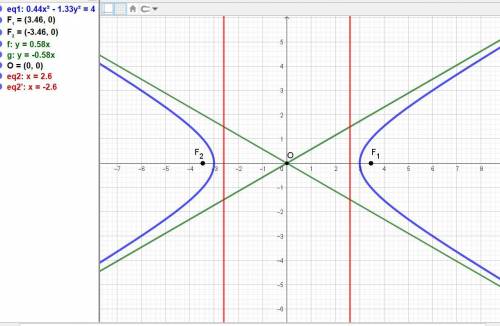
ответ: (x²/3²) - (y²/(√3)²) = 1.
Эксцентриситет гиперболы равен е = с/а = 2√3/3.
Уравнения асимптот у = +-(√3/3)x.
Координаты фокусов F1,F2 = (+-2√3; 0).
Уравнения директрис х = +-a²/c = +-3√3/2.
ответ: Теорема Фалеса-Если на одной стороне угла отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
Объяснение:1) Т.к. КМ-средняя линия, то КМ║ВС, КМ║АД,к-середина АВ, N-середина СД.
2)Т.к. АК=КВ и КО║ВС , то по т. Фалеса , АО=ОС. Значит КО-средняя линия ΔАВС. По т. о средней линии треугольника КО=1/2*ВС ,7=0,5*ВС ,ВС=14.
3)Т.к. СМ=МД и ОМ║АД, то по т. Фалеса , АО=ОС. Значит МО-средняя линия ΔАДС. По т. о средней линии треугольника МО=1/2*АД ,13=0,5*АД ,АД=26.