Его можно получить из графика гиперболы , которая лежит во 2 и 4 четвертях, т.к. k= -4<0, путём сдвига на 1 единицу влево вдоль оси ОХ . И тогда асимптотами новой гиперболы будут прямые, заданные уравнениями х= -1 и у=0 .
Можно найти координаты некоторых точек этой гиперболы, задавая значения переменной "х" и получая значения переменной "у" : (0,-4) , (3,-1) , (-3,2) , (-5,1)
A) Область определения функции D(х)=R Область значений E(у)=[0; +∞) Нули функции: х=0 Промежутки знакопостоянства: у>0 при х∈(-∞;0)∪(0+∞) Функция убывает при х∈(-∞; 0). Функция возрастает при х∈(0; +∞) Функция ограничена снизу: у≥0 Экстремумы функии: у[min]=0 Функция непрерывна. Функция чётная(график симметричен относительно оси Оу) Функция непериодична. б) Область определения функции D(х)=R Область значений E(у)=(-∞; 0) Нули функции: х=0 Промежутки знакопостоянства: у<0 при х∈(-∞;0)∪(0+∞) Функция убывает при х∈(0; +∞). Функция возрастает при х∈(-∞; 0) Функция ограничена сверху: у≤0 Экстремумы функии: у[max]=0 Функция непрерывна. Функция чётная(график симметричен относительно оси Оу) Функция непериодична.
Путешествие для меня - это лучший сбежать от повседневных трудностей.
Так прекрасно и невероятно понимать, что ты можешь увидеть множество мест, разные страны, удивительных людей, стать свидетелем чудес этого мира: Пустыни Сахара в северной Африке, Тадж Махалу в Индии, Пирамидам в Египте, замку Нойшванштайн в Баварии, Германия.
Если ты являешься счастливчиком, обладающим деньгами, временем и желанием, то можешь устремиться вдаль от своего родного города или деревни, странствуя по Африке, Австралие, Европу, Азие, Южной и Северной Америке - обогнуть весь мир.
В настоящее время путешествие так популярно особенно среди людей - жителей мегаполисов. Главная причина - их невыносимая усталость от постоянного проживания в огромных, загрязненных, шумных, густозаселенных городах как Москва, Мехико, Пекин, Нью-Йорк.
Многие любят спокойный тихий отдых на песчаном берегу рядом с глубоким зелёным морем.
Объяснение:
График функции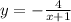 - это график гиперболы.
- это график гиперболы.
Его можно получить из графика гиперболы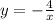 , которая лежит во 2 и 4 четвертях, т.к. k= -4<0, путём сдвига на 1 единицу влево вдоль оси ОХ . И тогда асимптотами новой гиперболы будут прямые, заданные уравнениями х= -1 и у=0 .
, которая лежит во 2 и 4 четвертях, т.к. k= -4<0, путём сдвига на 1 единицу влево вдоль оси ОХ . И тогда асимптотами новой гиперболы будут прямые, заданные уравнениями х= -1 и у=0 .
Можно найти координаты некоторых точек этой гиперболы, задавая значения переменной "х" и получая значения переменной "у" : (0,-4) , (3,-1) , (-3,2) , (-5,1)