т о биссектрисе
BE/EA =BC/CA =4/5
т Менелая
AD/DC *CF/FE *EB/BA =1 => 1/1 *CF/FE *4/9 =1 => CF/FE =9/4
Площади треугольников с равными высотами относятся как основания.
S(AEF)=x, S(CDF)=S(ADF) =y
S(AFC)/S(AEF) =CF/FE =9/4 =2y/x => S(AEF)/S(CDF) =x/y =8/9
Другое решение
BF/FD =BC/CD =4 :5/2 =8/5 (т о биссектрисе)
S(BCF)/S(CDF) =BF/FD =8/5 => S(CDF)=5/8 S(BCF)
S(ABD)=S(CBD), S(AFD)=S(CFD) => S(BCF)=S(BAF)
BE/EA =BC/CA =4/5 (т о биссектрисе)
S(BFE)/S(AEF) =BE/EA =4/5 => S(AEF) =5/9 S(BAF)
S(AEF)/S(CDF) =5/9 :5/8 =8/9
Объяснение:
1.
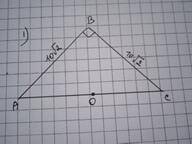
Дано: ΔАВС - прямокутний, ∠В=90°, АВ=ВС=10√2. R - ? r - ?
АС²=АВ²+ВС²=(10√2)² + (10√2)² = 200+200=400; АС=20.
Центр описаного кола припадає на середину гіпотенузи, отже
R=АО=ОС=20:2=10 од.
r=(a+b-c)/2=(10√2 + 10√2 - 20)\2 = (20√2 - 20)/2 = (20√2 - 1)/2 = 10√2 - 1 од.
2.
Катети трикутника а, в, гіпотенуза с. Тоді за умовою
а+в+с=24; а²+в²+с²=200; а²+в²=200-с², за теоремою Піфагора а²+в²=с²
200-с²=с²; 200=2с²; с²=100; с=10 см.
а+в+10=24; а+в=24-10=14 см.
Нехай а=х, тоді в=14-х.
х²+(14-х)²=10²
х²+196-28х+х²-100=0
2х²-28х+96=0
х²-14х+48=0
х=8 та х=6
а=8 см; в=6 см
S=1/2 * 8 * 6 = 24 cм²
Объяснение:
Решаем два уравнения.
1) Пересечение с осью ОУ при Х= 0. у = 1.
Точка А(0;1) - ответ.
2) Пересечение с осью ОХ при у= 0
0 = - 1,5*х +1 и 1,5*х = 1 и х = 1 : 1,5 = 2/3.
Точка В(2/3; 0)
Рисунок с графиком в приложении.
Для построения графика раздвинем точки.
х= -2, у = - 1,5*(-2) + 1 = 3+1 = 4
х = 2, у = - 1,5*2 + 1 = -3+1 = - 2